VM291

VM291
Force on the Boundary of a Semi-Infinite Body (Boussinesq Problem)

Overview

Reference:

Timoshenko, S.P., Goodier, J.N., Theory of Elasticity, McGraw-Hill, New York, pp. 398-402, 1970

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

Structural Infinite Solid (INFIN257)

2D 4-Node Structural Solid (PLANE182)

2D 8-Node Structural Solid (PLANE183)

Input Listing:

vm291.dat

Test Case

A point force is applied at the origin of a half-space 2D axisymmetric solid modeled with far-field domain. Determine the displacement in the Y-direction on nodes along the radial direction (at location Y = 0) and vertical direction (at location X = 0).

Figure 506: Finite and Infinite Element Mesh of the Problem (PLANE182 and INFIN257)

Figure 507: Finite and Infinite Element Mesh of the Problem (PLANE183 and INFIN257)

Material Properties [1]

Geometric Properties [1]

Loading [1]

Young’s modulus, E = 1.0

Poisson’s ratio, ν = 0.1

Radius of finite mesh = 4.0

Radius of infinite mesh = 4.0

Point load = 1.0

This is a unit independent problem.

Analysis Assumptions and Modeling Notes

The problem is solved for two cases:

Case 1: Using PLANE182 and INFIN257 elements
Case 2: Using PLANE183 and INFIN257 elements

The problem is composed with 12 axisymmetric finite element mesh (PLANE182 or PLANE183) with a radius of 4 from the origin, and 4 infinite element mesh (INFIN257) modeling the far-field domain with a radius of 4 extending from the finite element domain. The infinite element mesh is modeled using the EINFIN command. The UX degrees of freedom are constrained at location X = 0. The UY results are computed along the radial and vertical direction on the nodes belonging to the finite element mesh and then compared to the analytical results.

The analytic solution to compute vertical displacement for the problem of a point load on a half space is:

Where is the point load, is the Young’s modulus, is the Poisson’s ratio, and and are the radial and vertical distance from the point load. The above equation clearly shows the singularity at the point of application of the load ( and ), which indicates that the finite element results may not be close to the analytical solution a points close to the origin.

Results Comparison

Using PLANE182 and INFIN257 Elements
	Node Number	Target	Mechanical APDL	Ratio
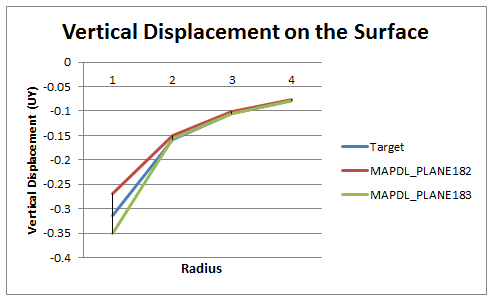
Vertical displacement (UY) on the surface (Y = 0)	5	-0.1576	-0.1504	1.048
	10	-0.1050	-0.1009	1.041
	15	-0.0788	-0.0771	1.021
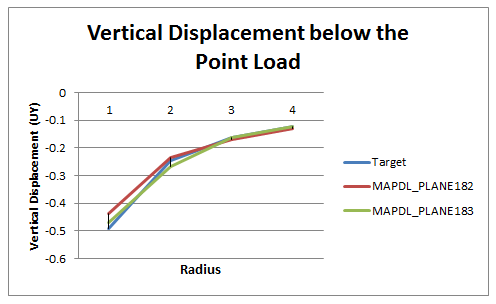
Vertical displacement (UY) below the point load (X = 0)	9	-0.2451	-0.2351	1.042
	14	-0.1634	-0.1688	0.968
	19	-0.1225	-0.1292	0.949
Using PLANE183 and INFIN257 Elements
	Node Number	Target	Mechanical APDL	Ratio
Vertical displacement (UY) on the surface (Y = 0)	10	-0.1576	-0.1575	1.001
	23	-0.1050	-0.1058	0.993
	37	-0.0788	-0.0787	1.002
Vertical displacement (UY) below the point load (X = 0)	19	-0.2451	-0.2663	0.920
	33	-0.1634	-0.1619	1.010
	47	-0.1225	-0.1225	1.000

Figure 508: UY Results Along Radial Direction (Y = 0)

Figure 509: UY Results Along Vertical Direction (X = 0)