VM284
VM284
Acceleration Solution in Response Spectrum Analysis Using
Missing Mass Method
Test Case
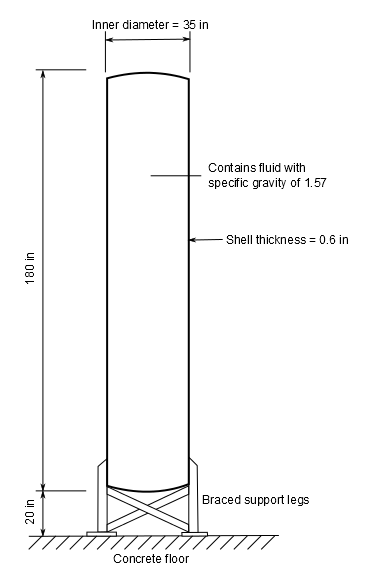
Single point acceleration response spectrum analysis is performed on a vertical tank model that is 200 inches tall and 35 inches in diameter by exciting the structure in the global Z-direction. The tank is supported by a braced leg support and is filled with a fluid with a specific gravity of 1.57. The spectrum analysis is performed with the first four modes and missing mass to account for the higher modes. The modes are combined using the SRSS mode combination method and the absolute acceleration at different elevation points of the structure is obtained by summing the SRSS modal response with the absolute missing mass response. The accelerations are compared against the reference values shown in Column 9 of Table 1 in the reference document.
| Material Properties | Geometric Properties | Loading | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
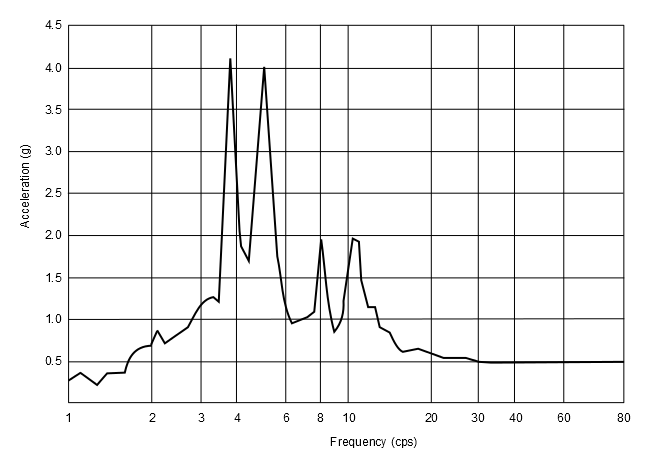
| Frequency vs. spectrum curve, refer to Figure 495: Frequency vs. Spectrum Values. |
Analysis Assumptions and Modeling Notes
The vertical tank is modeled with 3D 2-Node Beam Elements (BEAM188) with quadratic shape function and with circular tube cross section. The leg support is modeled with 3D 2-Node beam elements (BEAM188) with arbitrary cross section. The structural mass is equally distributed for the tank using MASS21 elements. The mass is determined from the specific gravity of the fluid and the volume of the tank. The first four modes are obtained using the Block-Lanczos eigensolver and these modes, along with the missing mass with ZPA value of 0.5, are used in the spectrum analysis to determine the absolute acceleration of the structure.