VM276
VM276
Moisture Diffusion in a Plate Under Constant Flux
Test Case
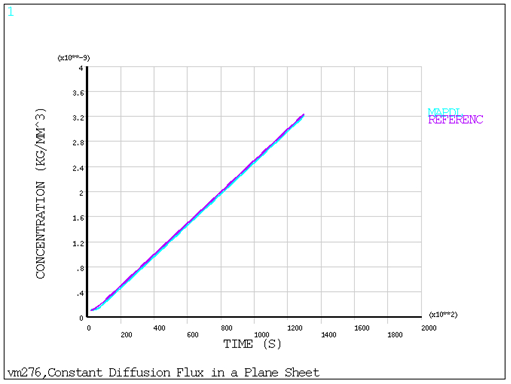
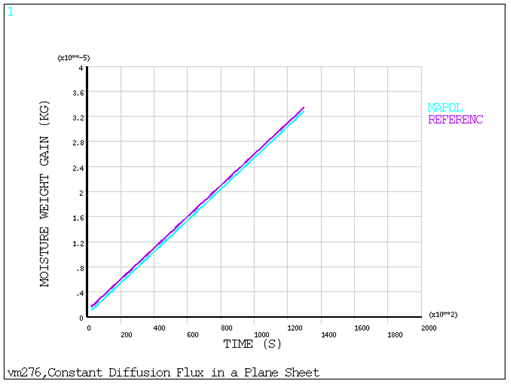
A plate of thickness 2l at an initial concentration C0 is subjected to an applied diffusion flux F0 at its surface (x = ± l). A time transient analysis (ANTYPE = 4) is performed at a run time of t=129600s and at a run time of t=90720s to determine the moisture concentration in the plate at location x=l/2. The total moisture weight gain is also determined at time t=90720s.
Analysis Assumptions and Modeling Notes
Constant diffusion flux F0 is applied as a surface load using the SF,,DFLUX command. The F0 is selected such that the concentration results will not exceed the saturated concentration Csat.
The normalized concentration approach is used for the analysis. Normalized initial concentration C0 is applied using the IC command. The saturated concentration Csat is defined as a material property (MP,,CSAT).
To calculate the moisture weight gain, the actual concentration (ETABLE,,SMISC,1) of each element is multiplied by the element’s volume. These individual element weight gains are then summed to give the total weight gain.
The target concentration solution is obtained from Eq. 4.55 given in the reference. The equation is truncated to five terms for target result calculation.
Where:
| CIC = The initial actual concentration of the plate, which is equal to C0*Csat. |
| x = X-location in plate. The value l/2 is used for target results calculations. |
The target total moisture weight gain solution is obtained by adding the initial moisture weight of the sheet to the below listed weight gain equation given in the reference.
Mt=M0+twh
Where:
M0 = the initial moisture weight at time t=0s, which is equal to 2*l*h*w*C0*Csat.