VM266

VM266
3D Crossing Beams in Contact with Friction

Overview

Reference:

G. Zavarise and P. Wriggers. " Contact with Friction Between Beams in 3D Space." International Journal for Numerical Methods in Engineering. 2000, vol. 49, pp. 977-1006.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

3D 2-Node Beam (BEAM188)

3D Line-To-Surface Contact (CONTA177)

3D Target Segment (TARGE170)

Input Listing:

vm266.dat

Test Case

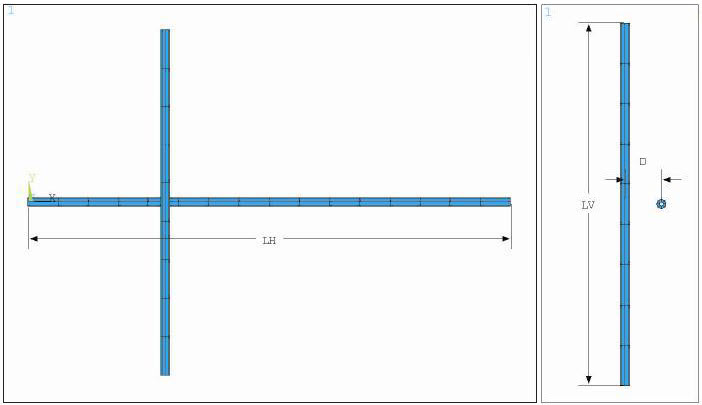
Two orthogonal beams with similar cross section and with an initial out-of-plane displacement are brought into contact by undergoing large displacements in 3D space. Normal and frictional contact forces are calculated at 0.5, 0.66, 0.83, and 1 second, and then compared against reference values.

Figure 462: Front view and lateral view of the crossing beams

Figure 463: Geometry and properties of the cross sections

Material Properties

Geometric Properties

Loading

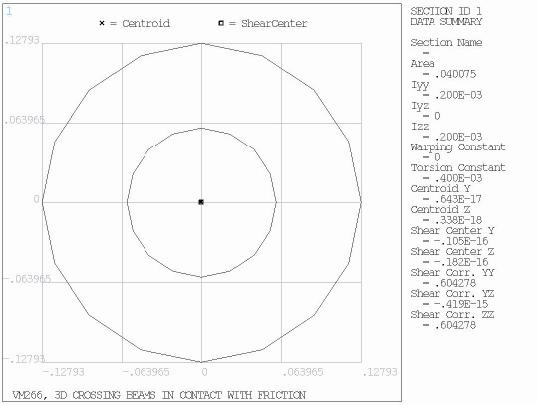
E=1.0 E+8 psi

ν = 0.0

µ = 0.1

LH=14 in

LV=10 in

D = 1 in

Cross-Section properties:

Ri = 0.06 in

Ro = 0.12793 in

A = 4.0 E-2 in²

I_yy = I_zz =2.0 E-4 in⁴

U_x = 0.18 in

U_z = 1.8 in

Analysis Assumptions and Modeling Notes

The beams are modeled using quadratic shape functions, with 16 equal length elements for the horizontal beam and 9 equal length elements for the vertical beam. The vertical beam is clamped at both ends, and the horizontal beam has the left end free and is restrained in all DOF at the right end except for the translational and out of plane directions. Displacement loading is applied at the right end of the horizontal beam to bring both beams into contact. Target elements (TARGE170) are defined on the vertical beam, and contact elements (CONTA177) are defined on the horizontal beam with penalty algorithm. A friction coefficient of 0.1 and penalty values for normal and tangential contact of 1.0E+4 are chosen according to the reference data. The normal and frictional contact forces are then calculated at different time steps and compared against the reference.

The model is solved again using traction-based crossing-beam contact: KEYOPT (3) = 3. An area factor, A = 5.71425 is used to scale the traction-based contact definition from the force-based contact definition. It has units m^-2 and is determined from the contact radius and element length (l): A = 1/(rl). This factor is used to scale the penalty values and results so that they use proper units.

Results Comparison

		Target	Mechanical APDL	Ratio
Normal Contact Force	NFORCE3 (t = 0.5s)	17.000	17.177	1.010
	NFORCE4 (t = 0.66s)	33.800	34.030	1.007
	NFORCE5 (t = 0.83s)	50.400	50.440	1.001
	NFORCE6 ( t= 1s)	67.000	66.295	0.989
Frictional Contact Force	TFORCE3 (t = 0.5s)	1.700	1.717	1.010
	TFORCE4 (t = 0.66s)	3.380	3.403	1.007
	TFORCE5 (t = 0.83s)	5.040	5.044	1.001
	TFORCE6 ( t= 1s)	6.700	6.629	0.989
Traction Based Contact – Normal Pressure	NPRES3 (t = 0.5s)	97.1422	98.1578	1.010
	NPRES4 (t = 0.66s)	193.1416	194.4582	1.008
	NPRES5 (t = 0.83s)	287.9982	288.2287	1.001
	NPRES6 ( t= 1s)	382.8547	378.8312	0.989
Traction Based Contact - Frictional Pressure	TPRES3 (t = 0.5s)	9.7142	9.8158	1.010
	TPRES4 (t = 0.66s)	19.3142	19.4458	1.008
	TPRES5 (t = 0.83s)	28.7998	28.8229	1.001
	TPRES6 ( t= 1s)	38.2855	37.8831	0.989