VM240

VM240
Thermal Expansion of Rigid Beams in a Composite Bar

Overview

Reference:

J.M. Gere, S.P. Timoshenko, Mechanics of Materials, 2^nd Edition, PWS Publishers, 1984, p. 20-21,71

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

Nonlinear (8-Node) Solid Elements (SOLID185)

Multipoint Constraint Elements - Rigid Beams (MPC184)

Input Listing:

vm240.dat

Test Case

A composite bar consists of two base materials with 25 rigid beams embedded along its length. A coefficient of thermal expansion is defined for only the rigid beams. Compare the stresses resulting in both solid composite materials when a temperature is applied.

Figure 405: Thermal Expansion of Composite Bar

Material Properties

Geometric Properties

E₁ = 10 x 10e⁶ psi

υ₁ = 0.3

E₂ = 5 x 10e⁶ psi

υ₂ = 0.3

α _x = α _y = α _z = 0.0003/in./°F (at 100 °F)

₁= 40 in.

w = 4 in.

h = 4 in.

T₁ = 0 °F

T₂ = 100 °F

Analysis Assumptions and Modeling Notes

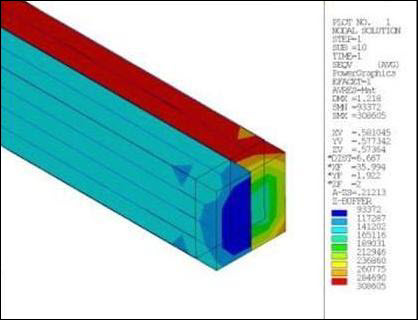
A composite bar with a 4" x 4" cross-section is modeled using SOLID185 elements. The bar consists of two different materials with the material properties E₁, E₂, υ₁, and υ₂ as shown above. Twenty five MPC184 rigid beam elements are then modeled running along the length of the bar. The rigid beam elements are given a coefficient of thermal expansion, α ₃. The bar is fixed in all DOF’s at one end. As a temperature is applied to the model, the rigid beam elements expand, in turn deforming the rest of the composite bar. As a result, two distinctly different stress levels can be seen through the bar’s cross-section. These stresses reflect the material property differences of the two materials making up the composite

The equations below are used to calculate theoretical stress values for comparison:

Results Comparison

	Target	Mechanical APDL	Ratio
1 - Equivalent Stress (von Mises)	300,000	297,700	0.992
2 - Equivalent Stress (von Mises)	150,000	148,900	0.992

Figure 406: Stress Results in Composite Material