VM214

VM214
Rotating Rod in a Uniform Magnetic Field

Overview

Reference:	Any basic electromagnetics textbook
Analysis Type(s):	Electromagnetic Static Analysis (ANTYPE = 0)
Element Type(s):	3D 20-Node Electromagnetic Solid Elements (SOLID236)
Input Listing:	vm214.dat

Test Case

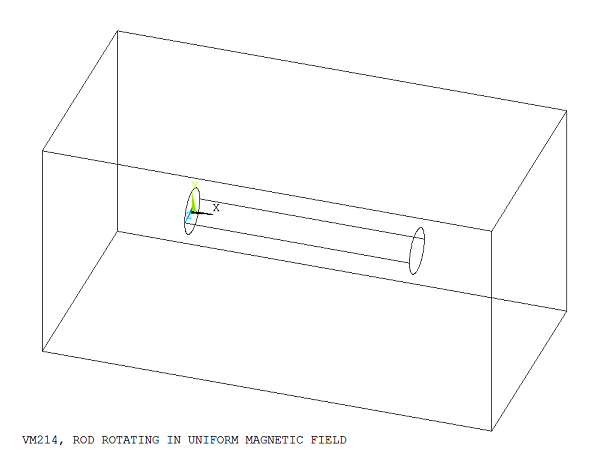
A conducting rod of length L (along the X-axis) and radius R is rotated about the Z-axis in a uniform magnetic field B_z with angular velocity Ω_z. Determine the induced voltage difference V between the ends of the rod.

Figure 341: Rotating Rod Surrounded by an Air Box

Figure 342: Finite Element Mesh of a Rod

Figure 343: Uniform Magnetic Field

Material Properties

Geometric Properties

Relative magnetic permeability, μ =1

Electrical resistivity, ρ = 1 Ohm-m

Length, L = 0.06 m

Radius, R = L/10 = 0.006 m

Magnetic field, B_z = 0.1 T

Angular velocity, Ω_z = 60 Hz or 377 rad/s

Analysis Assumptions and Modeling Notes

The model consists of a conducting rod surrounded by an open air box, as shown in Figure 341: Rotating Rod Surrounded by an Air Box. The rod is meshed with brick-shaped electromagnetic (KEYOPT(1) = 1) elements (SOLID236), and the surrounding air box with tetrahedron-shaped magnetic (KEYOPT(1) = 0) elements (SOLID236). Angular velocity Ω_z is specified using the BF,,VELO load to take into account the velocity effects in the conducting rod. The uniform magnetic field B_z is defined using the DFLX command. One end of the rod is electrically ground (D,,VOLT,0).

A linear static electromagnetic analysis is performed to determine the voltage distribution in the rod. The calculated voltage at the free end of the rod agrees with the analytical solution for the induced EMF:

Results Comparison

	Target	Mechanical APDL	Ratio
Voltage	0.06786	0.06770	0.998

Figure 344: Electric Potential Distribution in the Rod