Overview

Test Case

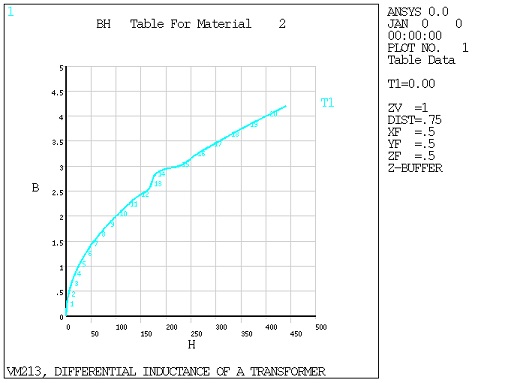
A transformer with a nonlinear iron core is wound with two separate coils. Coil 1 is excited by a current of 0.2 A, while coil 2 is excited by a current of 0.025 A. Calculate the differential self-inductance of both coil 1 and 2, as well as the differential mutual inductance between the two coils.

Figure 338: Schematic Drawing of a Transformer

Figure 339: Finite Element Model

Material Properties	Geometric Properties	Loading
where Bs = 2T Hs = 100 A/m	X = X1 = X2 = Y = Z = 0.015m Number of turns in coil 1, N1 = 10 Number of turns in coil 2, N2 = 20	Applied current in coil 1, I1 = 0.2 A Applied current in coil 2, I2 = 0.025 A

Analysis Assumptions and Modeling Notes

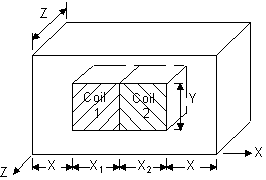
The half-symmetry model of the transformer consists of three blocks, which represent coil 1, coil 2, and the nonlinear iron core. The blocks are meshed using edge-based electromagnetic elements (SOLID236). A nonlinear magnetic static analysis is performed first to determine the operating point (I1, I2). The nonlinear analysis is followed by a linear perturbation magnetic static analysis with three load steps (I1, I0), (I0,I2), and (I1, I2), to determine the coil differential inductance with respect to an operating point (I1,I2). The differential inductance matrix is derived from the incremental energy of the system at these solution points. The incremental energy is calculated using the IENE element record.

Results Comparison

Figure 340: Harmonic Analysis of a Coaxial Cable