VM176

VM176
Frequency Response of Electrical Input Admittance

Overview

Reference: Y. Kagawa, T. Yamabuchi, "Finite Element Simulation of a Composite Piezoelectric Ultrasonic Transducer", IEEE Trans. Sonics and Ultrasonics, Vol. SU-2 No. 2, 1979, pg. 81.
Analysis Type(s): Full Harmonic Analysis (ANTYPE = 3)
Element Type(s):
3D Coupled-Field Solid Elements (SOLID5)
3D 20-Node Coupled-Field Solid (SOLID226)
3D 20-Node Structural Solid (SOLID186)
Input Listing: vm176.dat

Test Case

A composite piezoelectric transducer is made of a piezoceramic (NEPEC 6), aluminum, and an adhesive layer. Electrical terminals are attached to electroded surfaces of the piezoceramic where a potential V is applied. Determine the terminal input admittance Y over a frequency range spanning the first natural frequency.

Figure 263: Piezoelectric Transducer Problem Sketch

Piezoelectric Transducer Problem Sketch

Material PropertiesGeometric PropertiesLoading
For aluminum:
E = 7.03 x 1010 N/m
ρ = 2690 kg/m3
υ = 0.345
For adhesive:
E = 10 x 109 N/m2
ρ = 1700 kg/m3
υ = 0.38
For NEPEC 6:
See "Constitutive Matrices"
ha = 15.275 x 10-3 m
hn = 5 x 10-3 m
hb = 5.275 x 10-3 m
r = 27.5 x 10-3 m
V = 1 volt

Constitutive Matrices

NEPEC 6 "Stiffness" Matrix [c] x 10-10 N/m2

NEPEC 6 Piezoelectric Matrix [e] C/m2

NEPEC 6 Dielectric Matrix [εr]

Analysis Assumptions and Modeling Notes

The transducer has circumferential symmetry and is symmetric about the midplane, so the model is reduced to a single wedge of elements with an additional symmetry plane at z = 0. No internal losses (damping) are assumed. The top surface of the piezoceramic is electroded, resulting in an equipotential surface. The nodes modeling the surface have their voltage DOF coupled so that the applied potential load can be conveniently placed on a single node. The 1 volt potential load translates into a 0.5 volt potential gradient across the piezoceramic for the 1/2 symmetry model.

The TEMP and MAG degrees of freedom of SOLID5 are not used in this analysis.

Admittance Y is calculated as I/V where I is the current and V is the applied potential. The current I is related to the accumulated charge on the electrode surface as I = jωΣQi, where ω is the operating frequency, j is and ΣQi is the summed nodal charge (nodal reaction load). Since the nodal potentials are coupled, only the reaction "load" from the single node where the voltage is applied is required for the calculation. A series of calculations are made between 20 kHz and 54 kHz in POST26, which span the first natural frequency ( 44 kHz). The problem is first solved using SOLID5 elements and then using SOLID186 and SOLID226 elements.

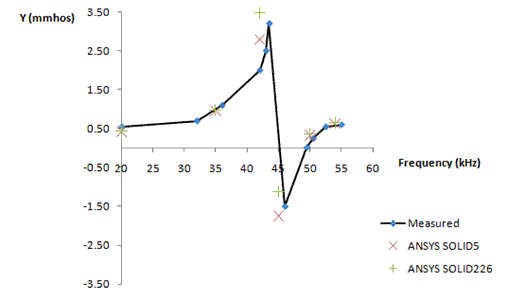
Results Comparison

Target[1]Mechanical APDL [2]Ratio
SOLID5
Y, mmhos @ 20kHz.41.431.047
Y, mmhos @ 35kHz.90.961.063
Y, mmhos @ 42kHz2.02.81.400
Y, mmhos @ 45kHz0.0-1.740.000
Y, mmhos @ 50kHz.39.320.833
Y, mmhos @ 54kHz.65.630.962
SOLID226
Y, mmhos @ 20kHz.41 .43 1.056
Y, mmhos @ 35kHz.90 .98 1.086
Y, mmhos @ 42kHz2.0 3.48 1.741
Y, mmhos @ 45kHz0.00 -1.13 0.000
Y, mmhos @ 50kHz.39 .37 0.961
Y, mmhos @ 54kHz.65.661.008

  1. The experimentally measured values are presented in graphical form in the reference. The results tabulated here are obtained from interpolation of the graphical data.

  2. Displayed graphically in Figure 264: Electrical Input Admittance vs. Frequency using SOLID5 and SOLID226 Elements.

Figure 264: Electrical Input Admittance vs. Frequency using SOLID5 and SOLID226 Elements

Electrical Input Admittance vs. Frequency using SOLID5 and SOLID226 Elements