A diffuse sound field is assumed to be a weak stationary random process. It is generally defined in terms of an infinite number of uncorrelated plane waves. The sound field is diffuse only if:

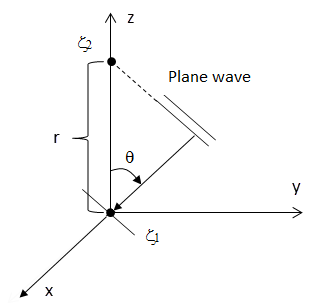
Considering plane waves at the two particular points, the first point is located at the origin while the second one is located at the (r, 90^o, 0,) in the spherical coordinate system with the position r = (r, , ). (Rafaely [422]and Van den Nieuwenhof et al. [423])

Figure 8.5: Plane Wave in Spherical Coordinates

The instantaneous pressure of the n ^th plane wave at the origin is expressed as:

(8–221)

The plane wave at the position (0, 0, z) can be retrieved by the pressure value at the origin:

(8–222)

The diffuse field pressure at the point is the superposition of an infinite number of plane waves from all directions:

(8–223)

The cross-correlation function of the pressures at the point and is expressed as:

(8–224)

Assuming that plane waves are uncorrelated and all signals have the same auto-correlation function , the cross-correlation function related to all plane waves directions with the element area on the unit sphere, which is replacing the element area in the summation, is:

(8–225)

After a change of the variable:

(8–226)

The cross-correlation function is rewritten as:

(8–227)

Because the power spectral density is the Fourier transformation of the auto-correlation function , the function is written as:

(8–228)

The cross-correlation function is given by:

(8–229)

Because the cross-power spectral density is the Fourier transformation of the cross-correlation function , that is:

(8–230)

The cross-power spectral density can be expressed as:

(8–231)

where:

is the acoustic wave number.

The diffuse sound field is approached by the asymptotic model of plane waves. The plane waves with random phases come from all directions in free space and superposition. The infinite number of plane waves is replaced with a sufficiently high number of plane waves for simulation purposes.

The reference sphere with the radius and origin are defined. Generally, the radius should be at least 50x the maximum dimension of the structural panel. The sphere surface is equally divided into elementary surfaces so that the plane waves carry the energy equally in all incident directions. In practice, the sphere surface is divided into parallel rings along the z axis of the global Cartesian coordinate system (default) or a user-specified local Cartesian coordinate system, and the program generates the elementary surfaces, each having nearly the same area.

Considering an elementary surface with an outward unit normal vector at the center of , the acoustic pressure at the point generated by the plane wave with the amplitude and phase propagating along direction, is defined by:

(8–232)

where:

(8–233)

The amplitude of each plane wave is defined by the reference power spectral density, , and expressed as:

(8–234)

In terms of the definition of diffuse sound field, the N phase angles are uniformly sampled in the range . The sampled diffuse sound field is given by:

(8–235)