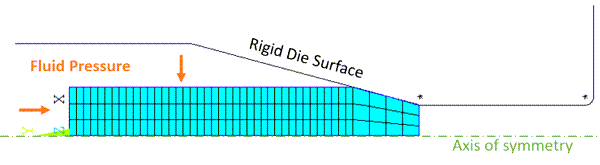
A 2D axisymmetric problem setup takes advantage of the cylindrical billet and conical die symmetry. The axisymmetric model consists of two parts, the billet and a rigid line representing the die surface:
| Billet and Die Dimensions | |
|---|---|
| Part | Dimension |
| Extrusion ratio | 2.5 |
| Billet radius | 5.534 mm |
| Die radius | 3.5 mm |
| Die angle | 15o |
| Elements used for Billet and Contact Pair | |
|---|---|
| Element | Key Options |
| PLANE182 |
KEYOPT(3) = 1 (axisymmetric) KEYOPT(6) = 1 (mixed u-P) |
| CONTA172 |
KEYOPT(2) = 3 (Lagrange and penalty) KEYOPT (5) = 1 (close gap) KEYOPT (14) = 0 |
| TARGE169 | -- |
The billet is modeled using PLANE182 axisymmetric elements. Mixed u-P formulation is specified because the billet material is used as incompressible hyperelastic-plastic.
The deformation of the material in the plug portion of the billet is not as large as the deformation of the main portion of the billet. During meshing, therefore, the elements in the plug portion maintain greater axial spacing. Because the element elongates more along the axial direction during meshing of the remainder of the billet, its size remains smaller than the size along the radial direction.
The surface-to-surface contact pair is defined using CONTA172 for the billet surface and TARGE169 as rigid lines:
A frictional interaction is defined for the contact pair and a friction coefficient of 0.1 is applied (MP). The contact formulation used is the Lagrange multiplier on contact-normal and penalty-on-tangent (KEYOPT (2) = 3 on CONTA172).