The first attempted solution is a static analysis that does not include any stabilization. In underconstrained models such as this one, the stiffness matrix may become close to singular during the Newton-Raphson iterations as indicated by the following warning message:
There is at least 1 small equation solver pivot term (e.g., at the UY degree of freedom of node 17617) which may indicate a numerically unstable model. Please check your results carefully.
Ignoring this warning leads either to convergence failure or convergence to an incorrect result.
Such problems often show different results when run on different compute cores or different platforms. For this particular model, the spring undergoes large tangential sliding as shown in the figure.
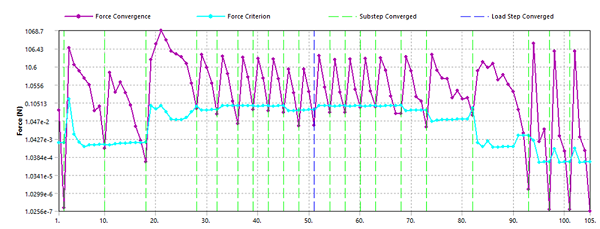
The problem is then solved using each of the five stabilization methods described in Analysis and Solution Controls. The convergence history plots are presented for each stabilization method, and the results are compared in Table 61.1: Summary of Results at End of First Load Step.
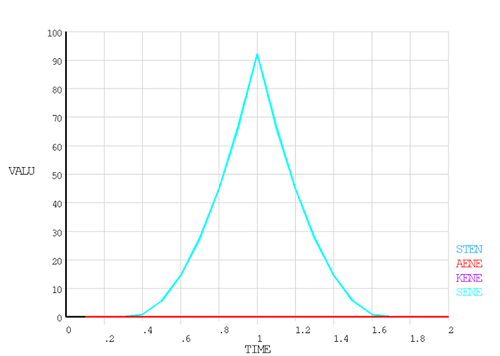
All stabilization methods yield nearly the same results at the end of the first load step. Artificial energies introduced due to the stabilization methods are negligibly small (see Table 61.1: Summary of Results at End of First Load Step and Figure 61.9: Energy History Plot for the Quasi-Static Transient). The cumulative iteration number and the artificial energy depend on the adjustment parameters of the stabilization method, as described below.
Weak Springs
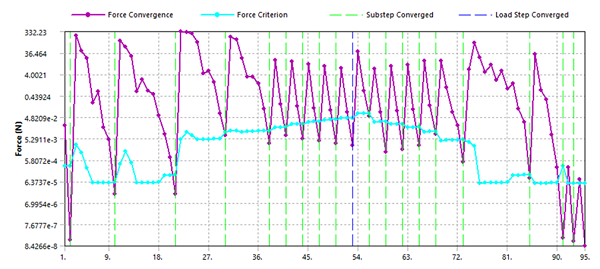
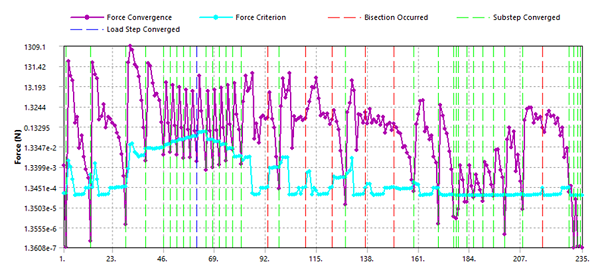
The weak springs method using default settings requires the maximum cumulative iterations (235) to converge. By increasing the stiffness of the springs, the solution converges in fewer iterations at the cost of extra stiffening.
Nonlinear Stabilization
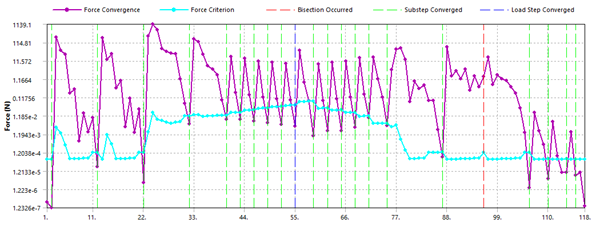
With the Ansys Mechanical application default settings, the nonlinear stabilization method takes 118 cumulative iterations. The number of iteration steps depends on these settings:
The stabilization control key (
Key= CONSTANT or REDUCE on the STABILIZE command)The stabilization control method and its associated value (
Method= ENERGY or DAMPING andVALUEon the STABILIZE command)The stabilization option for the first substep of the load step (
SubStpOpt= NO, MINTIME, or ANYTIME on the STABILIZE command)
For this analysis, Key = CONSTANT is chosen as the problem
is unstable during the entire analysis. For energy ratios
(VALUE) equal to 1e-2, 1e-4, and 1e-6, the total
iterations are 95, 118, and 147, respectively, with the same stiffness energy at the end
of the first load step (92.313 mJ). The STABILIZE command is:
stabilize,constant,energy,VALUE,,0.2If the SubStpOpt = ANYTIME option is used, the artificial
stabilization energy varies from 70 mJ to 85 mJ over the load steps for the default
energy ratio of 1e-4, therefore making the artificial energy dissipation too high. This
illustrates that you should be cautious when using the STABILIZE
command; tracking the energies is recommended.
Contact Stabilization
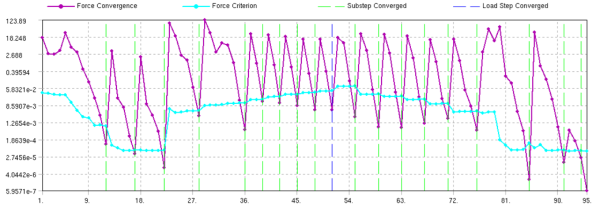
For the analysis with contact stabilization damping, the solution requires 83 iterations when KEYOPT(15) = 2 for the contact element and 95 iterations when KEYOPT(15) = 3. The contact damping can be controlled by contact element real constants FDMN and FDMT. Using KEYOPT(15) = 3 with real constant FDMT set to 100, 1, and .2, the total iterations are 165, 95, and 121, respectively, with total stiffness energies of 92.353 mJ, 92.045 mJ, and 92.134 mJ, respectively.
rmodif,6,32,x rmodif,8,32,x
Comparison of Results
Table 61.1: Summary of Results at End of First Load Step
| Analysis Method | Stiffness Energy (mJ) | Kinetic Energy (mJ) | Stabilization Energy (mJ) | Maximum Stress (MPa) | Total Iterations |
|---|---|---|---|---|---|
| Quasi-Static Transient | 92.211 | 0.051 | 0.000 | 34.95 | 95 |
| Weak Springs | 92.617 | 0.000 | 0.405 | 34.93 | 235 |
| Nonlinear Stabilization | 92.313 | 0.000 | 0.000 | 34.96 | 118 |
| Contact Stabilization | 92.045 | 0.000 | 0.000 | 34.894 | 95 |
| Low Speed Transient | 92.206 | 0.051 | 0.000 | 34.96 | 105 |
The quasi-static method does not require any adjustment parameters, and the converged solution is obtained with 95 iterations. The kinematic energy is negligible, and results are similar to a static analysis.
The low-speed transient method requires 105 iteration steps and yields results similar to the quasi-static transient.
Frictionless Contact Between the Spring and Blocks
For the case of frictionless contact (µ = 0.0) between the spring and the blocks (refer to Figure 61.1: 3D Model of a Coil Spring System), all static stabilization and weak spring methods fail to converge. Only the quasi-static and full transient formulations with alpha damping provide static-like results. The specified mass proportional damping stops the spring from flying away. The frictionless contact results are summarized below.
Table 61.2: Results at End of First Load Step - Frictionless Contact and Default Stabilization
| Analysis Method | Total Iterations | Alpha Damping (ALPHAD) | Stiffness Energy (mJ) |
|---|---|---|---|
| Quasi-Static Transient | 101 | α = 100 | 90.332 |
| Weak Springs | Not converged | - | - |
| Nonlinear Stabilization | Not converged | - | - |
| Contact Stabilization | Not converged | - | - |
| Low Speed Transient | 92 | α = 100 | 90.332 |