Following are the input listings for the example energy-calculation analyses:
The following input listing shows the model setup, the harmonic analyses, and
postprocessing. The analysis uses HROUT and
EngCalc = YES, then
EngCalc = NO.
/BATCH,LIST /COM, HARMONIC ANALYSIS /OUT,SCRATCH /PREP7 ET,1,COMBIN14,,,2 ET,2,MASS21,,,4 ! SYSTEM PARAMETERS SPRINGK = 200 ! SPRING CONSTANT MASS = 0.5 ! MASS KSI = 0.25 CVAL = 2*KSI*sqrt(SPRINGK*MASS) ! DAMPING R,1,SPRINGK,CVAL R,2,MASS N,1 N,4,1 FILL E,1,2 TYPE,2 REAL,2 E,2 ! MASS ELEMENT TYPE,1 REAL,1 E,2,3 ! SPRING ELEMENT TYPE,2 REAL,2 E,3 ! MASS ELEMENT TYPE,1 REAL,1 E,3,4 ! SPRING ELEMENT D,1,UY,,,4 D,1,UX,,,4,3 FINISH ! HARMONIC ANALYSIS WITH ENGCALC = YES /SOLU ANTYPE,HARMIC ! HARMONIC RESPONSE ANALYSIS HROPT,FULL ! FULL HARMONIC RESPONSE HROUT,,,,ON ! ENGCALC = YES HARFRQ,5,5 ! FREQUENCY 5 HZ NSUBST,1 F,2,FX,200 ! HARMONIC LOAD OF AMPLITUDE 200 KBC,1 ! STEP BOUNDARY CONDITION SOLVE FINISH /POST1 /OUT, /COM, /COM, ENERGY RESULTS WITH ENGCALC = YES SET,1,1 PRENERGY ! PRINT TOTAL ENERGIES *GET,AV_SENE_HARM,PRENERGY,,TOTE,1 ! AVERAGE STIFFNESS ENERGY *GET,AMPL_SENE_HARM,PRENERGY,,TOTE,2 ! AMPLITUDE STIFFNESS ENERGY *GET,PEAK_SENE_HARM,PRENERGY,,TOTE,3 ! PEAK STIFFNESS ENERGY *GET,PHASE_SENE_HARM,PRENERGY,,TOTE,4 ! PHASE OF STIFFNESS ENERGY *GET,AV_KENE_HARM,PRENERGY,,TOTE,5 ! AVERAGE KINETIC ENERGY *GET,AMPL_KENE_HARM,PRENERGY,,TOTE,6 ! AMPLITUDE KINETIC ENERGY *GET,PEAK_KENE_HARM,PRENERGY,,TOTE,7 ! PEAK KINETIC ENERGY *GET,PHASE_KENE_HARM,PRENERGY,,TOTE,8 ! PHASE OF KINETIC ENERGY *GET,DENE_CYCLE_HARM,PRENERGY,,TOTE,9 ! DAMPING ENERGY *GET,WEXT_CYCLE_HARM,PRENERGY,,TOTE,10 ! EXTERNAL WORK DELTA_PHASE_HARM = PHASE_KENE_HARM - PHASE_SENE_HARM ! PHASE BETWEEN KINETIC AND STIFFNESS ENERGIES SAVE SET,1,1,,2 PRENERGY /OUT,SCRATCH FINISH ! HARMONIC ANALYSIS WITH ENGCALC = NO /SOLU ANTYPE,HARMIC HROPT,FULL HROUT,,,,OFF ! ENGCALC = NO HARFRQ,5,5 ! FREQUENCY 5 HZ NSUBST,1 F,2,FX,200 KBC,1 SOLVE FINISH /POST1 /OUT, /COM, ENERGY RESULTS WITH ENGCALC = NO SET,1,1 PRENERGY ! PRINT TOTAL ENERGIES /OUT,SCRATCH *GET,SENE_HARM_REAL,PRENERGY,,TOTE,1 ! STIFFNESS ENERGY *GET,KENE_HARM_REAL,PRENERGY,,TOTE,2 ! KINETIC ENERGY /OUT SET,1,1,,2 PRENERGY /OUT,SCRATCH *GET,SENE_HARM_IMAG,PRENERGY,,TOTE,1 ! STIFFNESS ENERGY *GET,KENE_HARM_IMAG,PRENERGY,,TOTE,2 ! KINETIC ENERGY *DIM,LABEL,CHAR,2,1 *DIM,VALUE,,2,2 LABEL(1,1) = 'SENE' LABEL(2,1) = 'KENE' VALUE(1,1) = SENE_HARM_REAL VALUE(2,1) = KENE_HARM_REAL VALUE(1,2) = SENE_HARM_IMAG VALUE(2,2) = KENE_HARM_IMAG /OUT, /COM, /COM /COM,------------------- RESULTS COMPARISON ------------------- /COM, USING HROUT WITH EngCalc = NO /COM, /COM, | REAL | IMAGINARY *VWRITE,LABEL(1,1),VALUE(1,1),VALUE(1,2) (1X,A5,' ',F10.3,' ',F10.3) /COM,---------------------------------------------------------- /COM, /OUT FINISH
The following input performs the transient analysis using
TRNOPT with EngCalc = YES,
extracts the energy quantities from the steady-state part of the energies time
variation, and compares the results to those obtained from the harmonic analysis
using HROUT with EngCalc = NO.
/CLEAR,NOSTART
/COM, TRANSIENT ANALYSIS
/OUT,SCRATCH
RESUME ! RESUME FROM HARMONIC ANALYSIS
/SOLU
ANTYPE,TRANS
TRNOPT,FULL,,,,,,,,YES ! ENGCALC = YES
OUTRES,VENG,ALL ! WRITE ELEMENT ENERGIES ONLY
! TRANSIENT SETTINGS
NDIV=4100
DT=0.0005
TEND=NDIV*DT ! FINAL TIME IS 2.05s
! APPLY SINUSOIDAL LOAD
PI = ACOS(-1)
FREQ = 5 ! FREQUENCY, HERTZ
OMEGA = (2.0*PI)*FREQ ! IMPOSED CIRCULAR FREQUENCY, RADIAN/TIME
AMPL_FORCE = 200 ! FORCE AMPLITUDE
*DIM,FORCE,TABLE,NDIV,,,TIME
*DO,II,1,NDIV
TCURR = II*DT
FORCE(II,0) = TCURR
FORCE(II,1) = AMPL_FORCE*SIN(OMEGA*TCURR)
*ENDDO
! RESOLVE
TIMINT,ON
DELTIM,DT,DT,DT
TIME,TEND
F,2,FX,%FORCE%
SOLVE
FINISH
/POST26
JPGPRF,1000,100,1
/SHOW,JPEG
ENERSOL,2,SENE,,SE ! GET STIFFNESS ENERGY
ENERSOL,3,KENE,,KE ! GET KINETIC ENERGY
ENERSOL,4,DENE,,DE ! GET DAMPING ENERGY
ENERSOL,5,WEXT,,WE ! GET WORK
ADD,6,2,3,4,SE+KE+DE ! SUM STIFFNESS, KINETIC, DAMPING ENERGIES
/AXLAB,Y,ENERGIES
/GROPT,DIVX,5
/XRANGE,,2.05
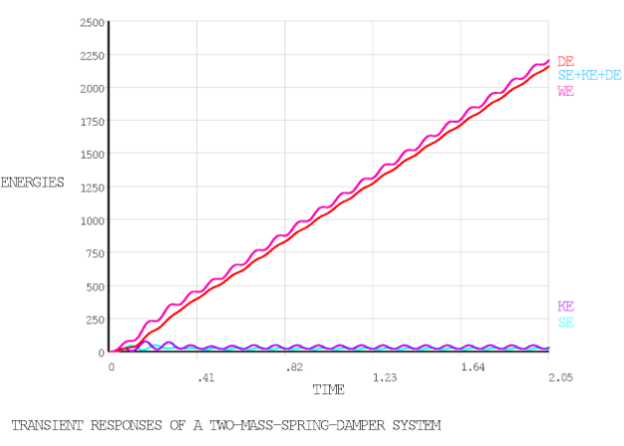
/TITLE, TRANSIENT RESPONSE OF A TWO-MASS-SPRING-DAMPER SYSTEM
PLVAR,2,3,4,6,5
! CALCULATE DAMPING ENERGY OVER A CYCLE
*GET,DENE_T2,VARI,4,REAL,2 ! GET DAMPING ENERGY AT T=2s
*GET,DENE_T1_8,VARI,4,REAL,1.8 ! GET DAMPING ENERGY AT T=1.8s
/OUT,
/COM,
/COM, DAMPING ENERGY OVER A CYCLE
DENE_CYCLE = DENE_T2-DENE_T1_8 ! IDENTIFIED DAMPING ENERGY OVER A CYCLE
/OUT,SCRATCH
! CALCULATE WORK DONE OVER A CYCLE
*GET,WEXT_T2,VARI,5,REAL,2 ! GET WORK ENERGY AT T=2s
*GET,WEXT_T1_8,VARI,5,REAL,1.8 ! GET WORK ENERGY AT T=1.8s
/OUT,
/COM,
/COM, WORK DONE OVER A CYCLE
WEXT_CYCLE = WEXT_T2-WEXT_T1_8 ! IDENTIFIED WORK OVER A CYCLE
/OUT,SCRATCH
! CALCULATE AVERAGE, AMPLITUDE, PEAK STIFFNESS ENERGY
*GET,SENE_T2,VARI,2,REAL,2 ! GET STIFFNESS ENERGY AT T=2s
*GET,SENE_T1_95,VARI,2,REAL,1.95 ! GET STIFFNESS ENERGY AT T=1.95s
*DIM,TAB_SENE,ARRAY,NDIV+1,1 ! LOOK AT LAST 0.1s
VGET,TAB_SENE,2,1.95
VPUT,TAB_SENE,7,1.95
*GET,VMAX_SENE,VARI,7,EXTREM,VMAX ! TO IDENTIFY PEAK STIFFNESS
*GET,TMAX_SENE,VARI,7,EXTREM,TMAX ! AND CORRESPONDING TIME
/OUT,
/COM,
/COM, AVERAGE, AMPLITUDE, PEAK STIFFNESS ENERGY
AV_SENE = (SENE_T2+SENE_T1_95)/2 ! IDENTIFIED AVERAGE STIFFNESS ENERGY
AMPL_SENE = VMAX_SENE-AV_SENE ! IDENTIFIED AMPLITUDE STIFFNESS ENERGY
PEAK_SENE = VMAX_SENE ! IDENTIFIED PEAK STIFFNESS ENERGY
/OUT,SCRATCH
! CALCULATE AVERAGE, AMPLITUDE, PEAK KINETIC ENERGY
*GET,KENE_T2,VARI,3,REAL,2 ! GET KINETIC ENERGY AT T=2s
*GET,KENE_T1_95,VARI,3,REAL,1.95 ! GET KINETIC ENERGY AT T=1.95s
*DIM,TAB_KENE,ARRAY,NDIV+1,1 ! LOOK AT LAST 0.1s
VGET,TAB_KENE,3,1.95
VPUT,TAB_KENE,8,1.95
*GET,VMAX_KENE,VARI,8,EXTREM,VMAX ! TO IDENTIFY PEAK KINETIC
*GET,TMAX_KENE,VARI,8,EXTREM,TMAX ! AND CORRESPONDING TIME
/OUT,
/COM,
/COM, AVERAGE, AMPLITUDE, PEAK KINETIC ENERGY
AV_KENE = (KENE_T2+KENE_T1_95)/2 ! IDENTIFIED AVERAGE KINETIC ENERGY
AMPL_KENE = VMAX_KENE-AV_KENE ! IDENTIFIED AMPLITUDE KINETIC ENERGY
PEAK_KENE = VMAX_KENE ! IDENTIFIED PEAK KINETIC ENERGY
/OUT,SCRATCH
! CALCULATE PHASE BETWEEN KINETIC AND STIFFNESS ENERGIES
/OUT,
/COM,
/COM, PHASE OF STIFFNESS AND KINETIC ENERGIES
PHASE_SENE = -2*OMEGA*(TMAX_SENE-2)
PHASE_KENE = -2*OMEGA*(TMAX_KENE-2)
/COM,
/COM, PHASE BETWEEN KINETIC AND STIFFNESS ENERGIES
DELTA_PHASE = -2*OMEGA*(TMAX_KENE-TMAX_SENE)
/OUT,SCRATCH
! PLOT ENERGIES OBTAINED WITH TRANSIENT ANALYSIS
! VERSUS ENERGY COSINE WAVES WHOSE AVERAGE, AMPLITUDE AND PHASE
! ARE CALCULATED WITH HARMONIC ANALYSIS WITH ENGCALC = YES
*DIM,SENE_HARM,ARRAY,NDIV+1,1
*DIM,KENE_HARM,ARRAY,NDIV+1,1
*DO,II,1,NDIV
TCURR = II*DT
CALC = AV_SENE_HARM + AMPL_SENE_HARM*COS(2*OMEGA*TCURR + PHASE_SENE_HARM)
SENE_HARM(II) = CALC
CALC = AV_KENE_HARM + AMPL_KENE_HARM*COS(2*OMEGA*TCURR + PHASE_KENE_HARM)
KENE_HARM(II) = CALC
*ENDDO
VPUT,SENE_HARM,9,,,SE_HARM
VPUT,KENE_HARM,10,,,KE_HARM
/XRANGE,,2.05
/GROPT,DIVX,5
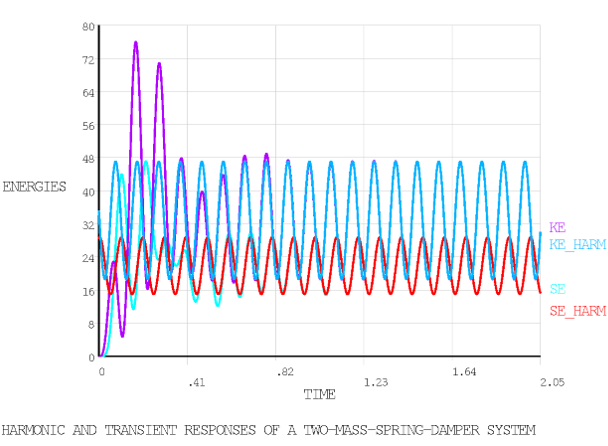
/TITLE, HARMONIC AND TRANSIENT RESPONSE OF A TWO-MASS-SPRING-DAMPER SYSTEM
PLVAR,2,3,9,10
FINISH
! PRINT RESULTS COMPARISON
*DIM,LABEL,CHAR,11,1
*DIM,VALUE,,11,2
LABEL(1,1) = 'SENE'
LABEL(2,1) = 'ASENE'
LABEL(3,1) = 'PSENE'
LABEL(4,1) = 'PHASE_SENE'
LABEL(5,1) = 'KENE'
LABEL(6,1) = 'AKENE'
LABEL(7,1) = 'PKENE'
LABEL(8,1) = 'PHASE_KENE'
LABEL(9,1) = 'DPHASE'
LABEL(10,1) = 'DENE'
LABEL(11,1) = 'WEXT'
VALUE(1,1) = AV_SENE_HARM
VALUE(2,1) = AMPL_SENE_HARM
VALUE(3,1) = PEAK_SENE_HARM
VALUE(4,1) = PHASE_SENE_HARM
VALUE(5,1) = AV_KENE_HARM
VALUE(6,1) = AMPL_KENE_HARM
VALUE(7,1) = PEAK_KENE_HARM
VALUE(8,1) = PHASE_KENE_HARM
VALUE(9,1) = DELTA_PHASE_HARM
VALUE(10,1) = DENE_CYCLE_HARM
VALUE(11,1) = WEXT_CYCLE_HARM
VALUE(1,2) = AV_SENE
VALUE(2,2) = AMPL_SENE
VALUE(3,2) = PEAK_SENE
VALUE(4,2) = PHASE_SENE
VALUE(5,2) = AV_KENE
VALUE(6,2) = AMPL_KENE
VALUE(7,2) = PEAK_KENE
VALUE(8,2) = PHASE_KENE
VALUE(9,2) = DELTA_PHASE
VALUE(10,2) = DENE_CYCLE
VALUE(11,2) = WEXT_CYCLE
/OUT,
/COM,
/COM
/COM,------------------- RESULTS COMPARISON -------------------
/COM,
/COM, | HARMONIC ANALYSIS | TRANSIENT ANALYSIS
*VWRITE,LABEL(1,1),VALUE(1,1),VALUE(1,2)
(1X,A5,' ',F10.3,' ',F10.3)
/COM,----------------------------------------------------------
/COM,
/OUT
FINISH
The following results-comparison topics for the energy-calculations problem are available:
The following table presents the results comparison, where consistency between harmonic and transient analyses can be observed:
| Energies | Harmonic Analysis | Transient Analysis |
|---|---|---|
| Average stiffness energy (SENE) | 21.878 | 21.873 |
| Amplitude stiffness energy (ASENE) | 6.889 | 6.888 |
| Peak stiffness energy (PSENE) | 28.766 | 28.762 |
| Phase stiffness energy | -0.292 | -0.283 |
| Average kinetic energy (KENE) | 32.839 | 32.832 |
| Amplitude kinetic energy (AKENE) | 14.261 | 14.259 |
| Peak kinetic energy (PKENE) | 47.100 | 47.092 |
| Phase kinetic energy | 1.373 | 1.382 |
| Δϕ | 1.664 | 1.665 |
| Damping energy (DENE) | 215.924 | 215.896 |
| External work (WEXT) | 215.924 | 215.919 |
The following figure shows the time variation of stiffness energy (SE), kinetic energy (KE), damping energy (DE), sum of stiffness, kinetic and damping energies (SE+KE+DE), and work of external load (WE). (Because SE+KE+DE superimposes on WE, it is not visible.)
This figure shows the time variation of stiffness energy (SE) and kinetic energy (KE) from the transient analysis, versus the cosine waves of stiffness energy (SE_HARM) and kinetic energy (KE_HARM) whose average, amplitude and phase are calculated in the harmonic analysis. (SE and SE_HARM, and KE and KE_HARM, superimpose in steady-state.)
The following table shows the energy results obtained from the harmonic
analysis using HROUT with EngCalc
= NO:
| Energies |
Harmonic Analysis Real part |
Harmonic analysis Imaginary Part |
|---|---|---|
| Average stiffness energy (SENE) | 15.280 | 28.475 |
| Average kinetic energy (KENE) | 35.646 | 30.032 |
The results indicate that more informative energy quantities are calculated
with EngCalc = YES.
Only the consistent average energy can be obtained by adding half of the average of the real part and half of the average of the imaginary part. Amplitude and phase cannot be calculated.