The Ramberg-Osgood material model describes a nonlinear stress-strain relationship and can have applications in metals that show a smooth elastic-plastic transition. While the application area for the model is in plasticity, it is actually an isotropic nonlinear elasticity model within the context of small strains. Accordingly, unloading occurs along the same path as the loading, and the material behavior is not history- or path-dependent.
The model can be used to simulate the nonlinear behavior of ductile metallic materials under monotonic proportional loading. It can capture the yield strength and isotropic hardening effects. As in von Mises plasticity models, the nonlinear effects are assumed to be purely deviatoric. In contrast to standard rate-independent plasticity models, the Ramberg-Osgood model does not introduce a yield surface to distinguish between linear and nonlinear behavior. The stress-strain relationship is nonlinear in the entire loading range. Furthermore, the model is not based on the concept of irreversible plastic strains. The plastic strains reported in postprocessing should be interpreted as a pseudo-plastic strain, as it returns to zero when the material is unloaded.
The model is used with elements having a three-dimensional or two-dimensional strain state, including 3D solid elements, and 2D plane elements with plane strain or axisymmetric conditions. Supported elements are listed in Material Model Support for Elements.
The following topics about the Ramberg-Osgood model are available:
In the general three-dimensional space, the nonlinear stress-strain relationship of the Ramberg-Osgood model can be expressed as:
with the hydrostatic pressure , the deviatoric stress
, and the von Mises stress
defined as:
where is the identity matrix.
| Ramberg-Osgood Material Parameters | |
|---|---|
| Young’s modulus | |
| Poisson’s ratio | |
| Yield strength | |
| Yield offset | |
| Hardening exponent | |
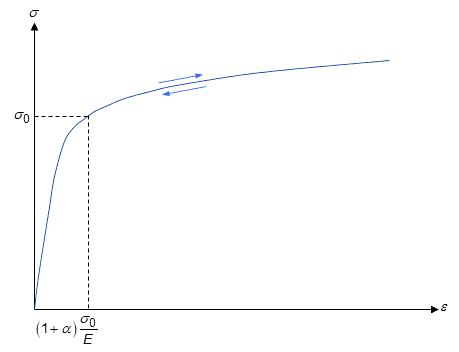
This figure shows the uniaxial nonlinear stress-strain behavior of the mode :
The plot illustrates that the relationship is nonlinear in the entire loading range.
The nonlinearity becomes significant when the stress exceeds the yield strength. The
yield offset defines the strain at yield strength. By using the additive split of strain
known from small-strain plasticity, the quantity can be interpreted as the plastic part and
as the elastic part.
The Ramberg-Osgood equation can be split into a volumetric part and a deviatoric part:
with the volumetric strain and the deviatoric strain
defined as:
The volumetric part of the equation is linear and can be directly solved for the
pressure :
The deviatoric part defines a nonlinear stress-strain relationship which is
iteratively solved using Newton’s procedure. In this context, an equivalent
one-dimensional relationship is obtained by introducing equivalent deviatoric strains and von Mises stress
:
If the von Mises stress is known, the deviatoric stress can be calculated as:
The material tangent can be obtained by differentiating the stresses with respect to the strains.
For postprocessing, the strain is additively split into an elastic part and a plastic part
(analogous to small-strain plasticity):
The strain quantities should be interpreted as a pseudo-elastic strain and a pseudo-plastic strain, as the plastic strain returns to zero when the material is unloaded.
Similarly, the strain-energy density , obtained by integrating stresses over strains, can be split into an
elastic part
and a plastic part
:
Specify the isotropic linear elastic material parameters (Young’s modulus and Poisson’s ratio) (MP,EX and MP,NUXY, or TB ,ELASTIC,,,,ISOT).
Define the Ramberg-Osgood material data table (TB,RO), then specify the strength-related parameters (TBDATA) via the following constants:
| Constant | Meaning | Property | Unit | Range |
|---|---|---|---|---|
| C1 | | Yield strength | Force/Length2 | |
| C2 | Yield offset | -- | ||
| C3 | Hardening exponent | -- |
The Ramberg-Osgood strength parameters can be defined as a function of temperature
(NTEMP on the TB command), with
temperatures specified for the table entries (TBTEMP).
Example 4.42: Ramberg-Osgood Model Material Constant Input
! Isotropic linear elasticity constants mp,ex ,1,390900 ! Young’s modulus [MPa] mp,nuxy,1,0.3 ! Poisson’s ratio ! Ramberg-Osgood strength constants tb,RO,1,,, tbdata,1,50 ! sigma_0 – yield strength [MPa] tbdata,2,0.5 ! alpha – yield offset tbdata,3,5 ! n – hardening exponent