The following examples are available:
This section describes a sample harmonic edge-based analysis, performed using Mechanical APDL.
This example examines the solution in the slot of an electric machine. For a specified AC (harmonic) current, the analysis calculates the magnetic field, energy, Joule heat losses and forces.
Figure 6.4: Current-Carrying Conductor in a Slot Within an Iron Region (in 3D Magnetostatics and Fundamentals of Edge-Based Analysis) and Figure 7.1: Volume Model of the Conductor illustrate, respectively, the problem domain and a volume model of the conductor within the slot in the domain.
The geometry is a block modeling a slot of an electrical machine. The z-axis coincides with the axis of the machine; l = .3 m is the length. The slot, with a depth of d = 0.1 m, is oriented in the x-axis. The width of the slot in the y direction is denoted by w = 0.01 m. A conductor with relative permeability, µr = 1, and resistivity, ρ = 1.0e-8, carries a current of 2236 A at a phase angle of 26.57° (corresponds in complex terms to 2000 + j1000 A). The analysis frequency is 3 Hz, which corresponds to a 5% slip frequency for a machine operating at 60 Hz.
The side and bottom of the slot are ideal iron. This is a flux-normal boundary condition (natural (Neumann) boundary condition); it is satisfied automatically without any prescription of an explicit boundary condition.
At the opening of the slot at x = d and at axial faces z = 0 and z = 1, the flux lines are parallel. This is an essential flux-parallel (Dirichlet) boundary condition; that is, its satisfaction is not automatic. You can prescribe it by setting (constraining) the flux-edge DOFs to a constant value, usually zero.
The example uses MKS dimensions (the default).
Parameters for the example are as follows:
| l = 0.3 | Length |
| d = 0.1 | Depth |
| w = 0.01 | Width |
| i = 2000 + j1000 | Current |
| mur = 1 | Relative magnetic permeability |
| ρ = 1.0e-8 | Electric resistivity (required for Joule loss) |
| n = 20 | Number of divisions through the slot depth |
| fr = 3 | Frequency |
Target data for the example are as follows:
Time-average Force in slot
FXrms = -46.89
Time-average Joule heat loss
PAVG = 25.9 watts
/TITLE, Harmonic analysis of a conducting plate /COM /NOPR ! *** Define model parameters l=0.3 ! length d=0.1 ! depth w=0.01 ! width mur=1 ! relative magnetic permeability rho=1.0e-8 ! electric resistivity (required for Joule loss) fr=3 ! rotor frequency at 5% slip curr=2000.0 ! current real curi=1000.0 ! current imaginary n=20 ! meshing parameter pi=3.1415926 mu0=pi*4.0e-7 ! free space permeability ! *** create model /PREP7 ET,1,236,1 KEYO,1,2,2 ! timie-integrated VOLT, symmetric system KEYO,1,8,1 ! calculate Lorentz force MP,MURX,1,mur MP,RSVX,1,rho BLOCK,0,d,0,w,0,l LSEL,S,LOC,X,d/2 LESIZE,ALL,,,n LSEL,ALL ESIZE,,1 VMESH,ALL FINI /SOLU ANTYP,HARM HARFR,fr ! *** Apply Dirichlet boundary condition NSEL,S,LOC,X,d NSEL,A,LOC,Z,0 NSEL,A,LOC,Z,l D,ALL,AZ,0 NSEL,S,LOC,Z,0 D,ALL,VOLT,0 NSEL,S,LOC,Z,l CP,1,VOLT,ALL *get,n1,node,,num,min F,n1,AMPS,curr,curi NSEL,ALL SOLVE FINI ! *** Extract solution /POST1 SET,1,1 ETABLE,fxr,FMAG,X PRETAB,fxr POWERH SSUM FINI ! *** Extract solution /POST1 SET,1,1 ETABLE,fxr,FMAG,X PRETAB,fxr POWERH SSUM FINI
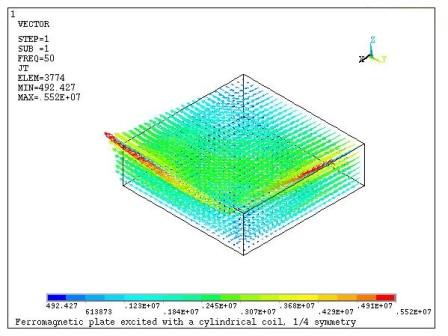
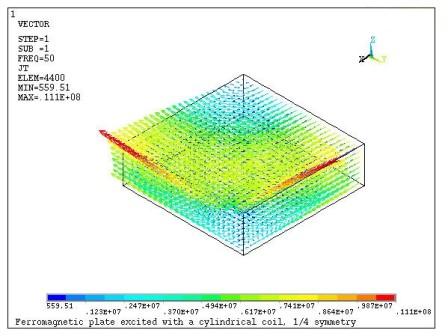
This example problem considers eddy currents in a ferromagnetic plate excited by a coil. A detailed model description can be found in "Challenges of Magnetic Quasi-Stationary Field Computations in Industrial Power Devices" by B. Cranganu-Cretu, J. Smajic and H. Nordborg, Proc. 12th International Symposium on Numerical Field Calculation in Electrical Engineering, pp. 313-317 (2006).
A 0.1 x 0.1 x 0.015 m ferromagnetic plate with electrical conductivity σ = 6.66e6 S/m and relative magnetic permeability of μ = 200 is excited by a cylindrical coil placed at a distance d = 0.05 m from the plate. The coil of height hc = 0.1 m with inner and outer radii of ri = 0.05 m and ro = 0.06 m respectively is energized by an rms current I = 1e5 A at 50 Hz.
A harmonic electromagnetic analysis is performed to determine the eddy current loss in a ferromagnetic plate. Only a quarter symmetry sector is considered for the analysis (Figure 7.2: Finite Element Model of the Ferromagnetic Plate and Coil). The coil and the plate are enclosed in an air box of size 0.5 x 0.5 x 0.4 m. Flux parallel boundary conditions are imposed on the exterior surface of the air enclosure.
Both the coil and the ferromagnetic plate are modeled using the electromagnetic analysis option (KEYOPT(1) = 1) of SOLID236. In addition, KEYOPT(5) is set to 1 for the coil to suppress the eddy currents. The air box is modeled using the magnetic analysis option KEYOPT(1) = 0.
The POWERH command macro is used to calculate the time-averaged (rms) power loss in the plate. Taking into account the symmetry factor, the power loss is found to be Pav=131.9 watts. The real and imaginary components of eddy current density in the plate are shown in Figure 7.3: Eddy Currents Distribution in the Plate (Real Solution) and in Figure 7.4: Eddy Currents Distribution in the Plate (Imaginary Solution), below.
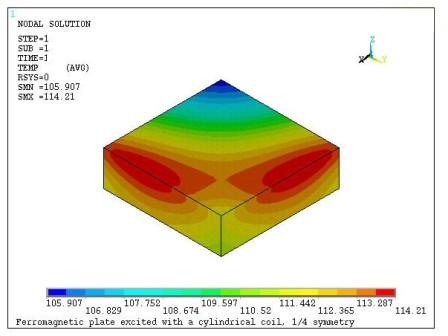
The electromagnetic analysis is followed by a steady-state thermal analysis to determine the temperature distribution in the plate due to Joule heating produced by the eddy currents. The ambient temperature is assumed to be 70 °C. The thermal conductivity and convection coefficient of the plate are taken to be k=50 watts/(m°C) and h=100 W/(m2°C) respectively.
The time-averaged Joule heat generation rate is transferred to the thermal SOLID90 model using the LDREAD,HGEN command. The resulting steady-state temperature distribution is shown in Figure 7.5: Temperature Distribution in the Plate . The average calculated temperature in the plate is Tav=110.1 °C
/title, Ferromagnetic plate excited with a cylindrical coil, 1/4 symmetry /nopr /VIEW,1,1,1,1 /VUP,1,Z /SHOW,win32c ! use /SHOW,x11c for X Window System /CONT,1,18 ! *** Problem parameters ! Ferromagnetic plate: lp=0.1 ! length, m hp=0.015 ! height, m eszp=0.002 ! element size, m sigp=6.66e6 ! conductivity, S/m mu_fer=200 ! relative permeability k=50 ! thermal conductivity, W/m_C h=100 ! convection coefficient, W/(m^2_C) ! Coil: ri=0.05 ! inner radius, m ro=0.06 ! outer radius, m hc=0.1 ! height, m d=0.05 ! distance between the coil and the plate,m eszc=0.005 ! element size, m frq=50 ! frequency, Hz I=1e5 ! rms coil current, A mu_coil=1 ! relative permeability ! Air box: la=0.5 ! length, m ha1=0.05 ! lower height, m ha2=0.35 ! upper height, m esza=0.03 ! element size, m mu_air=1 ! relative permeability sigc=2e-8 ! conductivity, S/m Tamb=70 ! ambient temperature,C /com, /com, *** Eddy current analysis /com, /PREP7 et,1,236,1 ! AZ-VOLT - ferromagnetic plate et,2,236,1,,,,1 ! AZ-VOLT (no eddy currents) - coil et,3,236 ! AZ - air block,0,lp/2,0,lp/2,0,hp ! plate cylinder,ri,ro,hp+d,hp+d+hc,0,90 ! coil block,0,la/2,0,la/2,-ha1,ha2 ! air vovlap,all numcmp,all mp,murx,1,mu_fer mp,rsvx,1,1/sigp mp,murx,2,mu_coil mp,rsvx,2,sigc mp,murx,3,mu_air type,1 mat,1 esize,eszp vmesh,1 type,2 mat,2 esize,eszc vmesh,2 msha,1,3D type,3 mat,3 esize,esza vmesh,3 asel,s,,,11 nsla,s,1 cp,1,volt,all f,ndnext(0),amps,I*sqrt(2) ! rms asel,s,,,12 nsla,s,1 d,all,volt,0 nsel,all asel,s,,,3 asel,a,,,5 nsla,s,1 d,all,volt,0 nsel,all nsel,s,ext d,all,az,0 ! Flux-parallel magnetic BC nsel,all allsel fini /SOLU antyp,harm harf,,frq solve fini /POST1 set,1,1 esel,s,mat,,1 ! select the plate POWERH ! calculate rms power loss plve,jt,,,,vect,elem,on ! plot eddy currents (real part) set,1,1,,1 plve,jt,,,,vect,elem,on ! plot eddy currents (imag part) alls fini /com, /com, Ansys computed power loss = %Pavg*4% watts /com, /com, *** Thermal analysis /com, /PREP7 ddele,all,az vsel,s,volu,,1 eslv et,1,90 LDREAD,hgen vsel,inve vclear,all alls etdele,2,3 mp,kxx,1,k nsel,s,ext sf,all,conv,h,Tamb nsel,all fini /SOLU anty,static solve fini /POST1 set,1,1 plnsol,temp nsort,temp *get,minTemp,sort,,min *get,maxTemp,sort,,max avTemp=(minTemp+maxTemp)/2 /com, /com, Average temperature of the plate = %avTemp% (C) /com, fini
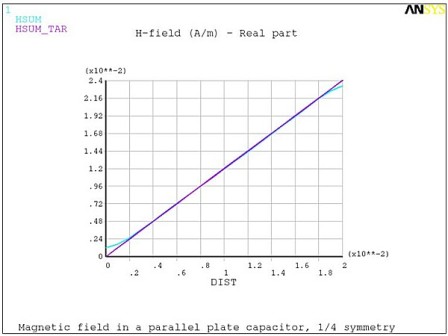
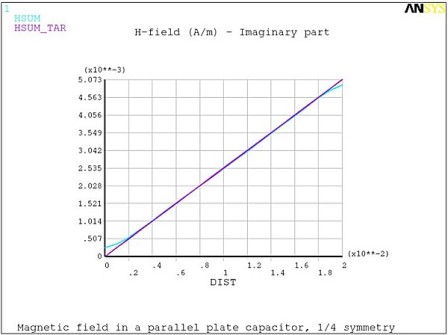
This example problem demonstrates the calculation of the magnetic field induced by both the conduction and displacement currents in a parallel plate capacitor filled with a lossy dielectric. Simulation results are compared to the analytical solution.
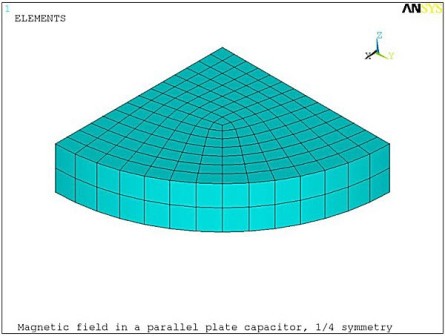
A parallel plate capacitor of radius a = 2 cm and thickness d = 0.5 cm is filled with a lossy dielectric with relative permittivity ε = 3.8 and electrical resistivity ρ = 1000 Ωm. The capacitor is driven by a time-harmonic electric field of magnitude Eo = 2400 V/m at frequency f = 1 MHz. A harmonic electromagnetic analysis is performed to determine the magnetic field induced in the capacitor as a function of distance r from the axis. Only a quarter symmetry sector is considered for the finite element model (Figure 7.6: Finite Element Model of the Lossy Capacitor).
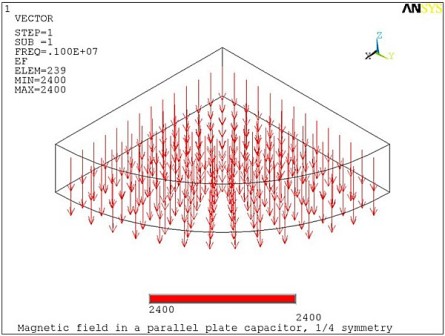
The capacitor is modeled using the electromagnetic analysis option (KEYOPT(1) = 1) of SOLID236. Flux parallel magnetic boundary conditions (AZ = 0) are imposed on the exterior surfaces of the capacitor and on the symmetry planes. The electrodes are defined by coupling the electric potential degree of freedom (VOLT) on the circular surfaces of the capacitor. The electric potential difference Eo*d is applied across the electrodes to create a uniform electric field (Figure 7.7: Electric Field in the Capacitor).
The total current density
induced in the lossy dielectric is composed of the conduction
current density (real part)
and the displacement current density (imaginary part)
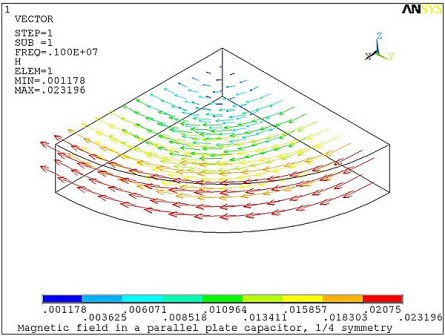
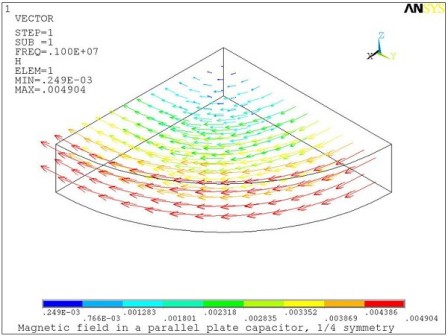
Note that the operating frequency f is low enough to allow neglecting the eddy currents contribution to the conduction current Jc. The conduction and displacement currents induce the real (Figure 7.8: Magnetic Field Induced by the Conduction Current) and imaginary (Figure 7.9: Magnetic Field Induced by the Displacement Current.) magnetic fields, respectively.
Using the Ampere's circuital law:
the real and imaginary parts of the magnetic field magnitude can be expressed respectively as follows:
and
These analytical expressions were used to demonstrate the agreement between the Mechanical APDL calculated and the target magnetic field as a function of distance r from the axis. (Figure 7.10: Computed and Analytical Real Magnetic Fields Hr and Figure 7.11: Computed and Analytical Imaginary Magnetic Field Hi )
/title, Magnetic field in a parallel plate capacitor, 1/4 symmetry /VIEW,1,1,1,1 /VUP,1,Z /com, /com, Problem parameters: Pi=acos(-1) a=2.e-2 ! radius, m d=0.5e-2 ! thickness, m epsr=3.8 ! relative permittivity rho=1000 ! electrical resistivity, Ohm*m E=2400 ! electric field V/m f=1.e6 ! frequency, Hz eps0=8.854e-12 ! free space permittivity, F/m Jc=E/rho ! conduction current density (Re) Jd=2*Pi*f*epsr*eps0*E ! displacement current density (Im) /nopr /PREP7 et,1,SOLID236,1 ! AZ+VOLT mp,perx,1,epsr mp,rsvx,1,rho mp,murx,1,1 cyl4,,,,,a,90,d esize,d/2 vmesh,all ! Electric boundary conditions and loads nsel,s,loc,z,0 cp,1,volt,all ! define bottom electrode *get,n_grd,node,0,num,min ! get master node on bottom electrode nsel,s,loc,z,d cp,2,volt,all ! top electrode *get,n_load,node,0,num,min ! get master node on top electrode nsel,all d,n_grd,volt,0 ! ground bottom electrode d,n_load,volt,E*d ! apply voltage load to top electrode ! Magnetic boundary conditions for 1/4 symmetry model nsel,s,loc,z,0 nsel,a,loc,z,d csys,1 nsel,a,loc,x,a csys,0 d,all,az,0 ! flux-parallel BCs nsel,all fini /solu antype,harm harfrq,,f outres,all,all kbc,1 ! stepped load solve fini /com, /com, Compare Mechanical APDL calculated and Expected H-field /com, /post1 path,path1,2,10,20 ppath,1,,0,0,0 ppath,2,,0,a,0 /com, /com, - Real solution /com, set,1,1 plvect,ef,,,,vect,elem,on ! electric field plvect,jt,,,,vect,elem,on ! conduction current plvect,h,,,,vect,elem,on ! magnetic field pdef,Hsum,h,sum,avg pcalc,add,Hsum_tar,s,,Jc/2 /tlabel,-0.2,0.8,H-field (A/m) - Real part plpath,Hsum,Hsum_tar prpath,Hsum,Hsum_tar /com, /com, - Imaginary solution /com, set,1,1,,1 plvect,js,,,,vect,elem,on ! displacement current plvect,h,,,,vect,elem,on ! magnetic field pdef,Hsum,h,sum,avg pcalc,add,Hsum_tar,s,,Jd/2 /ann,dele /tlabel,-0.2,0.8,H-field (A/m) - Imaginary part plpath,Hsum,Hsum_tar prpath,Hsum,Hsum_tar /ann,dele fini
This example problem demonstrates an harmonic analysis of a transformer.
A transformer consists of primary and secondary coils wound around a ferromagnetic core of high permeability μ. The coils have the same inner and outer radii R1 = 1.5 cm and R2 = 2 cm, respectively, and same height H = 4 cm. The primary coil is characterized by resistance RP = 24 Ω and the number of turns NP. The secondary coil resistance is RS = RP(NS/NP), where NS is the number of turns in the secondary coil. An additional high resistance R = 10000 Ω is attached to the secondary coil to minimize the output current.
The primary coil is energized with an alternating voltage of magnitude V = 1 Volt and frequency f = 50 Hz. The electric current in the primary coil creates a time-harmonic magnetic flux in the core, which induces a voltage in the secondary coil. A harmonic stranded coil analysis is performed to determine the voltage and electromotive force (EMF) induced in the secondary coil. A parametric analysis is also performed to determine how the core permeability μ and the ratio of the number of turns in the coils NS/NP affect the ratio of voltages in the secondary and primary coils.
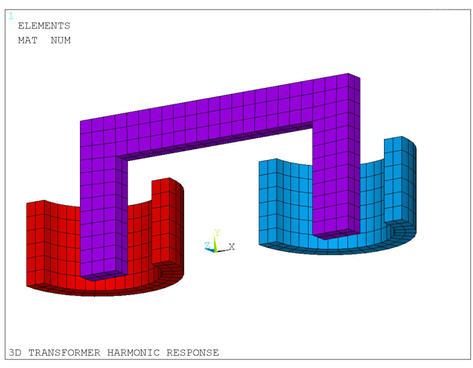
The coils are modeled using the stranded coil option (KEYOPT(1) = 2) of SOLID236. The core and the surrounding air are modeled using the magnetic option (KEYOPT(1) = 0) of SOLID236. The resistance attached to the secondary coil is modeled using the resistor option (KEYOPT(1) = 0) of CIRCU124. Only a quarter symmetry sector is considered for the finite element model (Figure 7.12: Finite Element Model of the Transformer (1/4 Symmetry)). Flux parallel magnetic boundary conditions (AZ = 0) are imposed on the exterior surfaces of the air domain and on the symmetry planes. The VOLT and EMF degrees of freedom are coupled in the coils.
The first harmonic analysis (see the Command Listing) was performed with a core relative permeability μ = 100000 and a coil turn ratio NS/NP = 200. The resulting voltage and EMF in the coils are shown in the following table.
Table 7.2: Coil Voltage and EMF (μ = 100000 and NS/NP = 200)
| Coil | Voltage | EMF |
|---|---|---|
| Primary | 1+j*0 | 0.970+j*0.142 |
| Secondary | -1.919-j*0.281 | -1.937-j*0.284 |
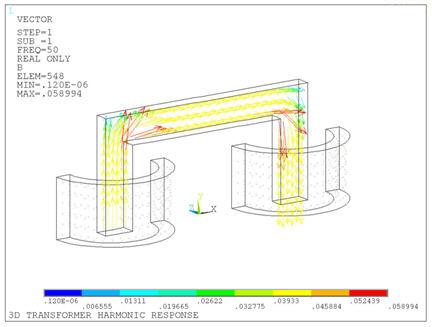
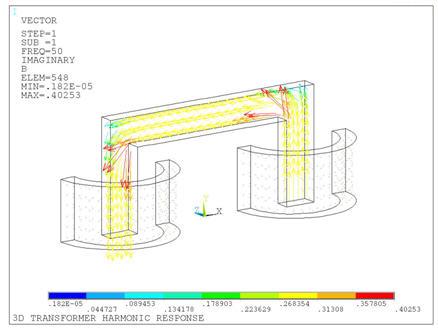
The magnetic flux in the core (real and imaginary) are shown in the following figures.
The current density in the primary and secondary coils (real and imaginary) are shown in the following figures.
As shown in the following tables, several subsequent harmonic analyses were performed to study the dependence of the voltage ratio in the coils as a function of core permeability and the ratio of the number of turns.
Table 7.3: Secondary and Primary Coil Voltage Ratio as a Function of Core Permeability μ (NS/NP = 200)
| Core permeability μ | Voltage Ratio VS/VP |
|---|---|
| 1000 | 0.129 |
| 10000 | 1.098 |
| 100000 | 1.94 |
Table 7.4: Secondary and Primary Coil Voltage Ratio as a Function of Ratio of Turns NS/NP (μ = 100000)
| Ration of Turns NS/NP | Voltage Ratio VS/VP |
|---|---|
| 200 | 1.94 |
| 300 | 2.84 |
| 400 | 3.67 |
/title, 3D Transformer Harmonic Response, 1/4 symmetry /vie,1,2,-1,3 /pnu,mat,1 /num,1 pi=acos(-1) ! *** Model parameters a_core=0.010 ! core cross-section width w_core=0.075 ! overall core width h_core=0.075 ! overall core height r1_coil=0.015 ! inner radius, both coils r2_coil=0.020 ! outer radius, both coils h_coil=0.040 ! height, both coils d_dmn=0.025 ! depth of surrounding domain esz1=a_core/3 ! element size, components esz2=3*esz1 ! element size, surrounding domain mu_core=100000 ! core permeability ! *** Primary coil Np=100 ! # of turns Rp=24 ! DC resistance (ohms) care_left=(r2_coil-r1_coil)*h_coil ! cross-sectional area volu_left=pi*(r2_coil**2-r1_coil**2)*h_coil ! volume Vp=1 ! voltage (V) ! *** Secondary coil Ns=200 ! # of turns Rs=Rp*(Ns/Np)**2 ! DC resistance (ohms) care_right=(r2_coil-r1_coil)*h_coil ! cross-sectional area volu_right=pi*(r2_coil**2-r1_coil**2)*h_coil ! volume R=1e4 ! resistance attached to the secondary coil frqncy=50 ! operating frequency (Hz) symm=4 ! symmetry factor /nopr ! *** Geometry /PREP7 vsel,none ! core bloc,-w_core/2,w_core/2,,h_core/2,-a_core/2,0 cm,scrap1_v,volu vsel,none bloc,-(w_core/2-a_core),w_core/2-a_core,,h_core/2-a_core,-a_core/2,0 cm,scrap2_v,volu cmse,s,scrap1_v cmse,a,scrap2_v vsbv,scrap1_v,scrap2_v cm,core_v,volu vatt,2,2,2 wpcs,-1,0 ! left coil ESYS wpof,-w_core/2+a_core/2 wpro,,-90 cswp,11,1 wpcs,-1,0 ! right coil ESYS wpof,w_core/2-a_core/2 wpro,,-90 cswp,12,1 csys vsel,none ! left coil wpcs,-1,11 cyli,r1_coil,r2_coil,0,h_coil/2,0,90 cyli,r1_coil,r2_coil,0,h_coil/2,90,180 vatt,3,3,3,11 vsel,none ! right coil wpcs,-1,12 cyli,r1_coil,r2_coil,0,h_coil/2,0,90 cyli,r1_coil,r2_coil,0,h_coil/2,90,180 vatt,4,4,4,12 alls cm,keep_v,volu *get,xmin,kp,,mnloc,x *get,xmax,kp,,mxloc,x *get,ymax,kp,,mxloc,y *get,zmin,kp,,mnloc,z wpcs,-1,0 ! surrounding domain vsel,none bloc,xmin-d_dmn,xmax+d_dmn,,ymax+d_dmn,zmin-d_dmn,0 cm,scrap_v,volu cmse,all vsbv,scrap_v,keep_v,,dele,keep cmse,u,keep_v cm,air_v,volu vatt,1,1,1 alls vplo ! *** FE model et,1,236 ! air mp,murx,1,1 et,2,236 ! core (laminated, non-conducting) mp,murx,2,mu_core et,3,236,2 ! left primary coil mp,murx,3,1 r,3,care_left,Np,volu_left,0,1,0 ! left coil data rmore,Rp,symm et,4,236,2 ! right secondary coil mp,murx,4,1 r,4,care_right,Ns,volu_right,0,1,0 ! right coil data rmore,Rs,symm ! *** Mesh numm,kp,1e-8,1e-8 esiz,esz1 vsel,s,mat,,3,4 vmes,all vsel,s,mat,,2 vswe,all vsel,s,mat,,1 msha,1 esiz,esz2 vmes,all alls ! *** Boundary conditions and loads asel,s,ext ! flux parallel exterior csys asel,u,loc,y da,all,az vsel,s,mat,,3 ! left primary coil alls,belo,volu cp,1,emf,all cp,2,volt,all nd_p=ndnext(0) alls vsel,s,mat,,4 ! right secondary coil alls,belo,volu cp,3,emf,all cp,4,volt,all nd_s=ndnext(0) alls d,nd_p,volt,Vp ! *** Circuit et,5,124,0 ! resistor connected to the secondary coil r,5,R *get,nmax,node,,num,max n,nmax+1,0,h_coil/2 type,5 real,5 e,nd_s,nmax+1 d,nmax+1,volt,0 ! ground csys eplo fini ! *** Solution /solu antype,harmonic harf,frqncy solve fini ! *** Post-processing /post1 set,,,,0 ! Real solution set Vp_real=volt(nd_p) Vs_real=volt(nd_s) /com, /com, *** Real solution /com, Vp = %Vp_real% /com, Vs = %Vs_real% /com, vsel,s,mat,,2,4 alls,belo,volu plve,jt,,,,vect,,on plve,b,,,,vect,,on plnsol,emf alls set,,,,1 ! Imaginary solution set Vp_imag=volt(nd_p) Vs_imag=volt(nd_s) /com, /com, *** Imag solution /com, Vp = %Vp_imag% /com, Vs = %Vs_imag% /com, vsel,s,mat,,2,4 alls,belo,volu plve,jt,,,,vect,,on plve,b,,,,vect,,on plnsol,emf alls Vp = sqrt(Vp_real**2 + Vp_imag**2) Vs = sqrt(Vs_real**2 + Vs_imag**2) /com, /com, *** Secondary to Primary Coil Voltage Ratio = %Vs/Vp% fini