This example considers the electric conduction problem with infinite boundaries described as problem # 476 in "Worked problems in Applied Mathematics," by N.N. Lebedev, I.P. Skalskaya, Y.S. Ufland, Dover Publications, Inc., NY, p. 226 (1979).
A DC current (I) enters ground of conductivity σ through a plate in the form of a disk of radius a. Find the distribution of electric current under the plate and calculate the resistance of the plate.
The geometric and electrical parameters are:
| Radius a = 1 cm |
| Applied current I = 5 mA |
| Soil electrical conductivity σ = 0.5 e-2 S/m |
Axisymmetric PLANE230 triangular elements model a rectangular area of width 2a and depth a below the circular electrode. A single layer of axisymmetric INFIN110 quadrilateral elements represents the exterior semi-infinite domain (IFE). The ratio of the IFE domain dimensions to the FE domain dimensions is equal to 1.8 (that is, the length of the infinite elements is approximately equal to the depth of the FE domain). The electrode is defined by coupling the VOLT degrees of freedom of the ground surface. The current load is applied as a concentrated nodal load.
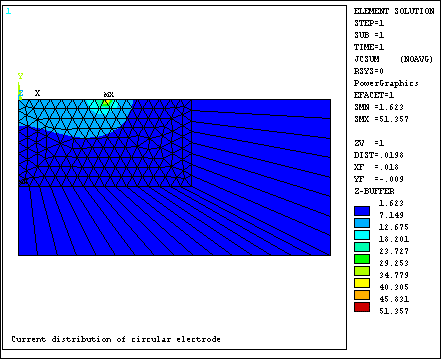
The electric current results are shown in the following figure.
The calculated resistance is 4943 Ohms. The expected result from the above reference is:
R = 1/(4σa) = 5000 Ohms
You can perform this electric conduction analysis using the Mechanical APDL commands shown below. Text prefaced by an exclamation point (!) is a comment.
/title, Current distribution of circular electrode ! Problem parameters I=5e-3 ! current, A sig=0.5e-2 ! conductivity of soil, S/m a=1e-2 ! disk radius, m w=2*a ! finite region width d=a ! finite region depth r=1.8 ! ratio infinite to finite /prep7 et,1,PLANE230,,,1 ! axisymmetric 8-node electric quad et,2,INFIN110,3,1,1 ! axisymmetric 8-node infinite electric quad mp,rsvx,1,1/sig ! resistivity input rect,,w,,-d ! enveloped area k,5,,r*(-d) k,6,r*w,r*(-d) k,7,r*w a,1,5,6,2 a,2,6,7,3 lesize,3,,,16 ! specify line divisions lesize,1,,,16 lesize,6,,,16 lesize,4,,,8 lesize,2,,,8 lesize,8,,,8 lesize,9,,,1 lesize,5,,,1 msha,1,2d ! mesh finite region with triangles type,1 amesh,1 mshk,1 ! mesh infinite region with quads msha,0,2d type,2 amesh,2,3 nummrg,node lsel,s,line,,6 ! flag exterior surface of INFIN elements lsel,a,line,,8 sfl,all,INF lsel,all nsel,s,loc,y,0 ! define electrode nsel,r,loc,x,0,a cp,1,volt,all ! couple VOLT dof n_load=ndnext(0) ! master node nsel,all fini /solu antype,static f,n_load,amps,I ! apply total current solve fini /post1 plesol,jc,sum ! plot electric current vector sum /com /com Calculated resistance R = %volt(n_load)/I% Ohm /com /com ************************************************************************** /com Expected results: R = %1/(4*sig*a)% Ohm /com ************************************************************************** finish