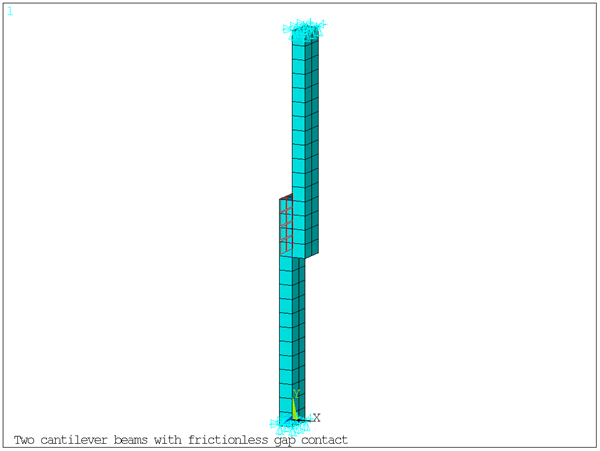
This example shows the nonlinear harmonic analysis of two cantilever beams with a gap contact between them using the harmonic balance method (HBM). Specifically, it demonstrates the following key points:
Frictionless gap contact using CONTA178 elements.
A 3D solid model.
Use of Component Mode Synthesis (CMS).
The example problem is presented in the following sections:
The example is modeled in two ways:
Full model.
Model with CMS reduction.
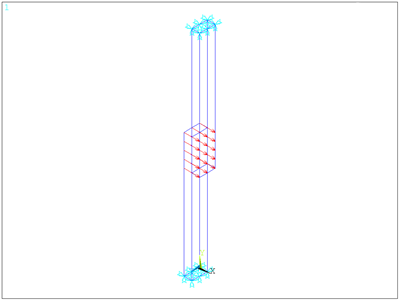
Two facing solid cantilever beams of length 0.16 m are meshed with SOLID185 elements. They are separated by a gap of size 1e-5 m and frictionless contact occurs on the last quarter of their length. The gap contact is defined with node-to-node CONTA178 elements.
An equivalent surface pressure is applied on the fourth quarter of the bottom beam to induce bending such that contact occurs.
The first bending frequency of the beams alone is f1 = 110.67 Hz. The HBM solution is computed in frequency range [0.80f1, 1.1f1] with NH = 9 harmonics to capture the contact response accurately.
The size of the model is reduced by generating one superelement for each beam. The master nodes are composed of the following:
boundary condition nodes
loading nodes
nodes used for nonlinear contact
one “observation” node on the top beam.
Like any CMS model, the number of modes used to generate the superelements must be sufficient to adequately represent the dynamics in the frequency range of interest. Here, 6 modes are used.
The number of nonlinear equations is the same for both the full and CMS models: (30 contact nodes)*(3 DOFs/node) = 90 transient equations.
However, CMS reduction of the linear part of the model further saves computation time by reducing the number of linear equations. The number of linear equations are as follows:
Full model: (192 nodes)*(3 DOFs/node)*(2*9+1 harmonics) = 10944 harmonic equations
CMS model: ((46 nodes)*(3 DOFs/node)+(6 modes/substructure)*2 substructures) *(2*9+1 harmonics) = 2850 harmonic equations
The number of equations information is printed in the output when the SOLVE command is issued.
This model is identical to that in Model with CMS Reduction except that a prestress load is applied on the tip of both beams. Linear perturbation substructuring analysis procedure is used to generate the prestressed superelements which are used in HBM analysis.
To download the .dat files used for this example problem, click the links below.
| hbm_example2a.dat - Full model |
| hbm_example2b.dat - CMS reduced model |
| hbm_example2c.dat - prestressed CMS reduced model |
The contents of these files are listed below. The command listing shows in detail how to specify and run the HBM analysis. You can use them as templates and modify them to create a custom HBM analysis.
Input for the full model
/BATCH,LIST /TITLE, Two cantilever beams with frictionless gap contact /com ============================================================= /com DESCRIPTION: /com Harmonic Balance analysis of two facing solid cantilever /com beams separated by a gap and interacting with frictionless /com contact. /com - Case a: full model /com ============================================================= ! Model Parameters PI = ACOS(-1) E = 1E10 ! Young's modulus RHO = 2700 ! Density L = 0.01 ! Unit length OMG = 110.67*2*PI ! single beam 1st eigenfrequency KN = -1E5 ! contact normal stiffness GAP = 1E-5 ! gap size FEXT = 40 ! external force ! HBM and Continuation Parameters NH = 9 ! number of harmonics DS = 2.0 ! initial arc length (step length) DSMIN = DS/100 ! minimum arc length (step length) DSMAX = 2*DS ! maximum arc length (step length) FMIN = 0.80*OMG/(2*PI) ! Starting frequency FMAX = 1.10*OMG/(2*PI) ! Ending frequency /PREP7 ! element type ET,1,185 ET,2,178 KEYOPT,2,1 ,0 ! unidirectional KEYOPT,2,2 ,1 ! penalty-based method KEYOPT,2,4 ,0 ! gap size based on real constant GAP + node location KEYOPT,2,10,0 ! standard contact R,2,KN ! material MP,EX ,1,E MP,PRXY,1,0.3 MP,DENS,1,RHO MP,BETD,1,0.00005 ! model BLOCK,0,L,0,16*L,0,2*L ! bottom beam BLOCK,L+gap,2*L+gap,12*L,28*L,0,2*L ! top beam ESIZE,L TYPE,1 REAL,1 MAT ,1 VMESH,ALL ! gap contact VSEL,S,VOLU,,1,,,1 NSEL,R,LOC,X,L NSEL,R,LOC,Y,12*L,16*L CM,BEAM1_GAP,NODE ALLSEL VSEL,S,VOLU,,2,,,1 NSEL,R,LOC,X,L+GAP NSEL,R,LOC,Y,12*L,16*L CM,BEAM2_GAP,NODE ALLSEL CMSEL,S,BEAM1_GAP CMSEL,A,BEAM2_GAP TYPE,2 REAL,2 EINTF,1E-6,,,,GAP ALLSEL finish /SOLU ANTYPE,HARMIC HROPT,HBM,NH ! HBM Solve and number of harmonics HARFRQ,FMIN,FMAX HBMOPT,NR,10 HBMOPT,CONTSET,,DS,DSMIN,DSMAX HBMOPT,LIST ! boundary conditions NSEL,S,LOC,Y,0 NSEL,A,LOC,Y,28*L D,ALL,ALL ALLSEL ! loading - surface pressure - harmonic 1 loading NSEL,S,LOC,X,0 NSEL,R,LOC,Y,12*L,16*L SF,ALL,PRES,FEXT ALLSEL ND_BOT = NODE(0,16*L,L) ND_TOP = NODE(2*L+GAP,12*L,L) KBC,1 SOLVE FINISH /com /com _________ DIRECT POST-PROCESSING OF HARMONIC SOLUTION _________ /com /POST1 *GET,JOBN,ACTIVE,,JOBNAM FILE,%JOBN%_1hi0,rst SET,LIST SET,1,39 /VIEW,,0.1,0.25,1 /EDGE,,1 /DSCALE,,1E2 /TITLE, Two cantilever beams with frictionless gap contact /SHOW,PNG,REV PLNSOL,U,SUM /SHOW,CLOSE FINISH /com /com _________ POST-PROCESSING USING MACRO 'HBM_EXPA' _________ /com *GET,JOBN,ACTIVE,,JOBNAM HBM_EXPA,JOBN,ND_BOT,'U','X',NH,'minmax' *DIM ,_HBM_AMPL_BEAM ,TABLE,_NSS,2 *VFUN,_HBM_AMPL_BEAM(1,1),COPY ,_HBM_AMPL(1) ! save results for node %ND_BOT% (bottom beam) HBM_EXPA,JOBN,ND_TOP,'U','X',NH,'minmax' *VFUN,_HBM_AMPL_BEAM(1,2),COPY,_HBM_AMPL(1) ! save results for node %ND_TOP% (top beam) /SHOW,PNG,REV /AXLAB,X,FREQUENCY (HZ) /AXLAB,Y,AMPLITUDE /GCOLUMN,1,BOT_BEAM /GCOLUMN,2,TOP_BEAM *VPLOT,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),2 /SHOW,CLOSE /com /com Frequency (Hz) Amplitude of the response /com Bot. Beam | Top Beam /com *VWRITE,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),_HBM_AMPL_BEAM(1,2) (F16.8,2X,E16.8,2X,E16.8)
Input for the CMS model
/BATCH,LIST
/TITLE, Two cantilever beams with frictionless gap contact
/com =============================================================
/com DESCRIPTION:
/com Harmonic Balance analysis of two facing solid cantilever
/com beams separated by a gap and interacting with frictionless
/com contact.
/com - Case b: CMS model
/com =============================================================
! Model Parameters
PI = ACOS(-1)
E = 1E10 ! Young's modulus
RHO = 2700 ! Density
L = 0.01 ! Unit length
OMG = 110.67*2*PI ! single beam 1st eigenfrequency
KN = -1E5 ! contact normal stiffness
GAP = 1E-5 ! gap size
FEXT = 40 ! external force
! HBM and Continuation Parameters
NH = 9 ! number of harmonics
NMODE = 6 ! number of modes for CMS reduction
DS = 2.0 ! initial arc length (step length)
DSMIN = DS/100 ! minimum arc length (step length)
DSMAX = 2*DS ! maximum arc length (step length)
FMIN = 0.80*OMG/(2*PI) ! Starting frequency
FMAX = 1.10*OMG/(2*PI) ! Ending frequency
/PREP7
! element type
ET,1,185
! material
MP,EX ,1,E
MP,PRXY,1,0.3
MP,DENS,1,RHO
MP,BETD,1,0.00005
! model
BLOCK,0,L,0,16*L,0,2*L ! bottom beam
BLOCK,L+gap,2*L+gap,12*L,28*L,0,2*L ! top beam
ESIZE,L
TYPE,1
REAL,1
MAT ,1
VMESH,ALL
FINISH
SAVE,ALL3D,DB
PARSAV,,ALL3D,PARM
/com
/com ______________ GENERATION PASS - BOTTOM BEAM _____________
/com
/FILNAME,BEAM1
/SOLU
ANTYPE,SUBSTR
SEOPT,BEAM1,3,,,NONE ! generate stiffness, mass, and damping matrix
! (NONE = no files kept for expansion)
CMSOPT,FIX,NMODE
! master dofs
VSEL,S,VOLU,,1,,,1 ! gap contact nodes - bottom beam
NSEL,R,LOC,X,L
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM1_GAP,NODE
ALLSEL
NSEL,S,LOC,Y,0 ! boundary conditions - bottom beam
CM,BEAM1_BC,NODE
ALLSEL
NSEL,S,LOC,Y,12*L,16*L ! loading - bottom beam
NSEL,R,LOC,X,0
CM,BEAM1_LOAD,NODE
ALLSEL
CMSEL,S,BEAM1_GAP
CMSEL,A,BEAM1_LOAD
CMSEL,A,BEAM1_BC
M,ALL,ALL
ALLSEL
VSEL,S,VOLU,,1,,,1 ! select only nodes and elements for bottom beam
CM,BEAM1_ELEM,ELEM
solve
finish
/com
/com ______________ GENERATION PASS - TOP BEAM _____________
/com
/FILNAME,BEAM2
/SOLU
ANTYPE,SUBSTR
SEOPT,BEAM2,3,,,NONE ! generate stiffness, mass, and damping matrix
! (NONE = no files kept for expansion)
CMSOPT,FIX,NMODE
! master dofs
VSEL,S,VOLU,,2,,,1 ! gap contact nodes - top beam
NSEL,R,LOC,X,L+GAP
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM2_GAP,NODE
ALLSEL
NSEL,S,LOC,Y,28*L ! boundary conditions - top beam
CM,BEAM2_BCLOAD,NODE
ALLSEL
TIP_NODE = NODE(2*L+GAP,12*L,L) ! tip node
CMSEL,S,BEAM2_GAP
CMSEL,A,BEAM2_BCLOAD
NSEL,A,NODE,,TIP_NODE
M,ALL,ALL
ALLSEL
VSEL,S,VOLU,,2,,,1 ! select only nodes and elements for top beam
CM,BEAM2_ELEM,ELEM
SOLVE
FINISH
/com
/com ______________ USE PASS _____________
/com
/CLEAR,NOSTART
/FILNAME,USE
PARRES,,ALL3D,PARM
/PREP7
! load SE
ET,10,50
TYPE,10
SE,BEAM1
SE,BEAM2
! create NL elements
ET,2,178
KEYOPT,2,1 ,0 ! unidirectional
KEYOPT,2,2 ,1 ! penalty-based method
KEYOPT,2,4 ,0 ! gap size based on real constant GAP + node location
KEYOPT,2,10,0 ! standard contact
R,2,KN
! gap contact
SELTOL,1E-6
NSEL,S,LOC,X,L
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM1_GAP,NODE
ALLSEL
NSEL,S,LOC,X,L+GAP
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM2_GAP,NODE
ALLSEL
CMSEL,S,BEAM1_GAP
CMSEL,A,BEAM2_GAP
TYPE,2
REAL,2
EINTF,1E-6,,,,GAP
ALLSEL
FINISH
/SOLU
ANTYPE,HARMIC
HROPT,HBM,NH ! HBM Solve and number of harmonics
HARFRQ,FMIN,FMAX
HBMOPT,NR,10
HBMOPT,CONTSET,,DS,DSMIN,DSMAX
HBMOPT,LIST
! boundary conditions
NSEL,S,LOC,Y,0
NSEL,A,LOC,Y,28*L
D,ALL,ALL
ALLSEL
! loading - surface pressure mimicked with nodal load
! FEXT is applied to nodes belonging to 1 loaded element
! 2*FEXT is applied to nodes belonging to 2 different loaded elements
! 4*FEXT is applied to nodes belonging to 4 different loaded elements
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,12*L,16*L
NSEL,R,LOC,Z,L
NSEL,U,LOC,Y,12*L
NSEL,U,LOC,Y,16*L
CM,CENTER_NODE,NODE
F,ALL,FX,4*FEXT*(8*L**2)/32
ALLSEL
NSEL,S,LOC,Y,12*L
NSEL,A,LOC,Y,16*L
NSEL,R,LOC,X,0
NSEL,U,LOC,Z,L
CM,CORNER_NODE,NODE
F,ALL,FX,FEXT*(8*L**2)/32
ALLSEL
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,12*L,16*L
CMSEL,U,CENTER_NODE
CMSEL,U,CORNER_NODE
CM,SIDE_NODE,NODE
F,ALL,FX,2*FEXT*(8*L**2)/32
ALLSEL
ND_BOT = NODE(0,16*L,L)
ND_TOP = NODE(2*L+GAP,12*L,L)
KBC,1
SOLVE
FINISH
/com
/com _________ POST-PROCESSING USING MACRO 'HBM_EXPA' _________
/com
/POST26
FILE,USE0,rst
JOBN='USE'
HBM_EXPA,JOBN,ND_BOT,'U','X',NH,'minmax'
*DIM ,_HBM_AMPL_BEAM ,TABLE,_NSS,2
*VFUN,_HBM_AMPL_BEAM(1,1),COPY ,_HBM_AMPL(1) ! save results for node %ND_BOT% (bottom beam)
HBM_EXPA,JOBN,ND_TOP,'U','X',NH,'minmax'
*VFUN,_HBM_AMPL_BEAM(1,2),COPY,_HBM_AMPL(1) ! save results for node %ND_TOP% (top beam)
/SHOW,PNG,REV
/AXLAB,X,FREQUENCY (HZ)
/AXLAB,Y,AMPLITUDE
/GCOLUMN,1,BOT_BEAM
/GCOLUMN,2,TOP_BEAM
*VPLOT,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),2
/SHOW,CLOSE
/com
/com Frequency (Hz) Amplitude of the response
/com Bot. Beam | Top Beam
/com
*VWRITE,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),_HBM_AMPL_BEAM(1,2)
(F16.8,2X,E16.8,2X,E16.8)
FINISH
Input for the Prestress CMS Model
/BATCH,LIST
/TITLE, Two cantilever beams with frictionless gap contact
/com =============================================================
/com DESCRIPTION:
/com Harmonic Balance analysis of two facing solid cantilever
/com beams separated by a gap and interacting with frictionless
/com contact.
/com - Case c: prestressed CMS model
/com =============================================================
! Model Parameters
PI = ACOS(-1)
E = 1E10 ! Young's modulus
RHO = 2700 ! Density
L = 0.01 ! Unit length
OMG = 110.67*2*PI ! single beam 1st eigenfrequency
KN = -1E5 ! contact normal stiffness
GAP = 1E-5 ! gap size
FEXT = 40 ! external force
! HBM and Continuation Parameters
NH = 9 ! number of harmonics
NMODE = 6 ! number of modes for CMS reduction
DS = 2.0 ! initial arc length
DSMIN = DS/100 ! minimum arc length
DSMAX = 2*DS ! maximum arc length
FMIN = 0.80*OMG/(2*PI) ! Starting frequency
FMAX = 1.10*OMG/(2*PI) ! Ending frequency
/PREP7
! element type
ET,1,185
! material
MP,EX ,1,E
MP,PRXY,1,0.3
MP,DENS,1,RHO
MP,BETD,1,0.00005
! model
BLOCK,0,L,0,16*L,0,2*L ! bottom beam
BLOCK,L+gap,2*L+gap,12*L,28*L,0,2*L ! top beam
ESIZE,L
TYPE,1
REAL,1
MAT ,1
VMESH,ALL
FINISH
/com
/com ______________ PRESTRESS PASS _____________
/com
/SOLU
ANTYPE,STATIC
RESCONTROL,LINEAR,ALL,1
! boundary conditions
NSEL,S,LOC,Y,0
NSEL,A,LOC,Y,28*L
D,ALL,ALL
ALLSEL
! prestress load
NSEL,S,LOC,Y,16*L
NSEL,R,LOC,X,0,L
SF,ALL,PRES,2E6
ALLSEL
NSEL,S,LOC,Y,12*L
NSEL,R,LOC,X,L+GAP,2*L+GAP
SF,ALL,PRES,2E6
ALLSEL
SOLVE
FINISH
SAVE,ALL3D,DB
PARSAV,,ALL3D,PARM
/com
/com ______________ GENERATION PASS - BOTTOM BEAM _____________
/com
! /FILNAME,BEAM1
/SOLU
ANTYPE,STATIC,RESTART,,,PERTURB
PERTURB,SUBSTR,,,DZEROKEEP
SOLVE,ELFORM
SEOPT,BEAM1,3,,,NONE ! generate stiffness, mass and damping matrix
! (NONE = no files kept for expansion)
CMSOPT,FIX,NMODE
! master dofs
VSEL,S,VOLU,,1,,,1 ! gap contact nodes - bottom beam
NSEL,R,LOC,X,L
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM1_GAP,NODE
ALLSEL
NSEL,S,LOC,Y,0 ! boundary conditions - bottom beam
CM,BEAM1_BC,NODE
ALLSEL
NSEL,S,LOC,Y,12*L,16*L ! loading - bottom beam
NSEL,R,LOC,X,0
CM,BEAM1_LOAD,NODE
ALLSEL
CMSEL,S,BEAM1_GAP
CMSEL,A,BEAM1_LOAD
CMSEL,A,BEAM1_BC
M,ALL,ALL
ALLSEL
VSEL,S,VOLU,,1,,,1 ! select only nodes and elements for bottom beam
CM,BEAM1_ELEM,ELEM
SOLVE
FINISH
/com
/com ______________ GENERATION PASS - TOP BEAM _____________
/com
/CLEAR,NOSTART
! /FILNAME,BEAM2
RESUME,ALL3D,DB
/SOLU
ANTYPE,STATIC,RESTART,,,PERTURB
PERTURB,SUBSTR,,,DZEROKEEP
SOLVE,ELFORM
SEOPT,BEAM2,3,,,NONE ! generate stiffness, mass and damping matrix
! (NONE = no files kept for expansion)
CMSOPT,FIX,NMODE
! master dofs
VSEL,S,VOLU,,2,,,1 ! gap contact nodes - top beam
NSEL,R,LOC,X,L+GAP
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM2_GAP,NODE
ALLSEL
NSEL,S,LOC,Y,28*L ! boundary conditions - top beam
CM,BEAM2_BCLOAD,NODE
ALLSEL
TIP_NODE = NODE(2*L+GAP,12*L,L) ! tip node
CMSEL,S,BEAM2_GAP
CMSEL,A,BEAM2_BCLOAD
NSEL,A,NODE,,TIP_NODE
M,ALL,ALL
ALLSEL
VSEL,S,VOLU,,2,,,1 ! select only nodes and elements for top beam
CM,BEAM2_ELEM,ELEM
SOLVE
FINISH
/com
/com ______________ USE PASS _____________
/com
/CLEAR,NOSTART
/FILNAME,USE
PARRES,,ALL3D,PARM
/PREP7
! load SE
ET,10,50
TYPE,10
SE,BEAM1
SE,BEAM2
! create NL elements
ET,2,178
KEYOPT,2,1 ,0 ! unidirectional
KEYOPT,2,2 ,1 ! penalty-based method
KEYOPT,2,4 ,0 ! gap size based on real constant GAP + node location
KEYOPT,2,10,0 ! standard contact
R,2,KN
! gap contact
SELTOL,1E-6
NSEL,S,LOC,X,L
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM1_GAP,NODE
ALLSEL
NSEL,S,LOC,X,L+GAP
NSEL,R,LOC,Y,12*L,16*L
CM,BEAM2_GAP,NODE
ALLSEL
CMSEL,S,BEAM1_GAP
CMSEL,A,BEAM2_GAP
TYPE,2
REAL,2
EINTF,1E-6,,,,GAP
ALLSEL
FINISH
/SOLU
ANTYPE,HARMIC
HROPT,HBM,NH ! HBM Solve and number of harmonics
HARFRQ,FMIN,FMAX
HBMOPT,NR,10
HBMOPT,CONTSET,,DS,DSMIN,DSMAX
HBMOPT,LIST
! boundary conditions
NSEL,S,LOC,Y,0
NSEL,A,LOC,Y,28*L
D,ALL,ALL
ALLSEL
! loading - surface pressure mimicked with nodal load
! FEXT is applied to nodes belonging to 1 loaded element
! 2*FEXT is applied to nodes belonging to 2 different loaded elements
! 4*FEXT is applied to nodes belonging to 4 different loaded elements
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,12*L,16*L
NSEL,R,LOC,Z,L
NSEL,U,LOC,Y,12*L
NSEL,U,LOC,Y,16*L
CM,CENTER_NODE,NODE
F,ALL,FX,4*FEXT*(8*L**2)/32
ALLSEL
NSEL,S,LOC,Y,12*L
NSEL,A,LOC,Y,16*L
NSEL,R,LOC,X,0
NSEL,U,LOC,Z,L
CM,CORNER_NODE,NODE
F,ALL,FX,FEXT*(8*L**2)/32
ALLSEL
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,12*L,16*L
CMSEL,U,CENTER_NODE
CMSEL,U,CORNER_NODE
CM,SIDE_NODE,NODE
F,ALL,FX,2*FEXT*(8*L**2)/32
ALLSEL
ND_BOT = NODE(0,16*L,L)
ND_TOP = NODE(2*L+GAP,12*L,L)
KBC,1
SOLVE
FINISH
/com
/com _________ DIRECT POST-PROCESSING _________
/com
/POST26
NUMVAR,200
FILE,USE_1hi0,rst ! select result file containing harmonic 1 results
NSOL,102,ND_BOT,u,x ! store and print frequency history results for harmonic 1
ABS ,102,102
NSOL,103,ND_TOP,u,x ! store and print frequency history results for harmonic 1
ABS ,103,103
/SHOW,png,rev
/AXLAB,X,Frequency (Hz)
/AXLAB,Y,Harmonic 1 - amplitude
PLVAR,102,103
/SHOW,close
PRVAR,102,103
FINISH
/com
/com _________ POST-PROCESSING USING MACRO 'HBM_EXPA' _________
/com
/POST26
FILE,USE0,rst
JOBN='USE'
HBM_EXPA,JOBN,ND_BOT,'U','X',NH,'minmax'
*DIM ,_HBM_AMPL_BEAM ,TABLE,_NSS,2
*VFUN,_HBM_AMPL_BEAM(1,1),COPY ,_HBM_AMPL(1) ! save results for node %ND_BOT% (bottom beam)
HBM_EXPA,JOBN,ND_TOP,'U','X',NH,'minmax'
*VFUN,_HBM_AMPL_BEAM(1,2),COPY,_HBM_AMPL(1) ! save results for node %ND_TOP% (top beam)
/SHOW,PNG,REV
/AXLAB,X,FREQUENCY (HZ)
/AXLAB,Y,AMPLITUDE
/GCOLUMN,1,BOT_BEAM
/GCOLUMN,2,TOP_BEAM
*VPLOT,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),2
/SHOW,CLOSE
/com
/com Frequency (Hz) Amplitude of the response
/com Bot. Beam | Top Beam
/com
*VWRITE,_HBM_FREQ(1),_HBM_AMPL_BEAM(1,1),_HBM_AMPL_BEAM(1,2)
(F16.8,2X,E16.8,2X,E16.8)
FINISH
Output contains information on the convergence, the arc length, and the maximum amplitude of each harmonic at each substep. The example output message below shows that the solver needed two iterations to converge.
RESIDUAL INFINITE NORM VALUE = 0.003732
ITERATION 1 COMPLETED
RESIDUAL INFINITE NORM VALUE = 8.863e-08
ITERATION 2 COMPLETED
>>> SOLUTION CONVERGED
CURRENT STEP SIZE = 10
** MAXIMUM AMPLITUDE OF DISPLACEMENT SOLUTIONS **
HARMONIC REAL IMAG
0 0.7646E-06
1 0.1620E-04 0.1836E-04
2 0.4504E-06 0.9648E-07
3 0.4688E-07 0.1278E-06
4 0.6442E-07 0.3625E-07
5 0.4176E-07 0.3909E-07
6 0.5943E-07 0.1138E-06
7 0.1696E-07 0.1060E-06
8 0.4490E-07 0.3106E-07
9 0.2315E-07 0.2209E-07
*** LOAD STEP 1 SUBSTEP 37 COMPLETED. FREQUENCY= 108.811
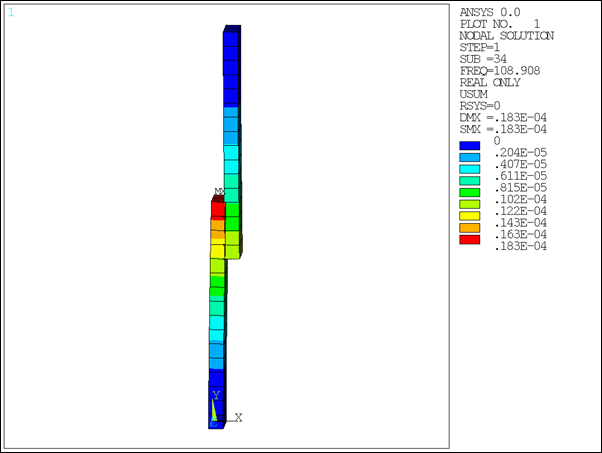
You can create displacement plots for a given harmonic at a selected frequency using direct postprocessing in /POST1 as shown below.
You can calculate the response amplitude using the HBM_EXPA macro, which performs postprocessing in a similar manner to example 1.
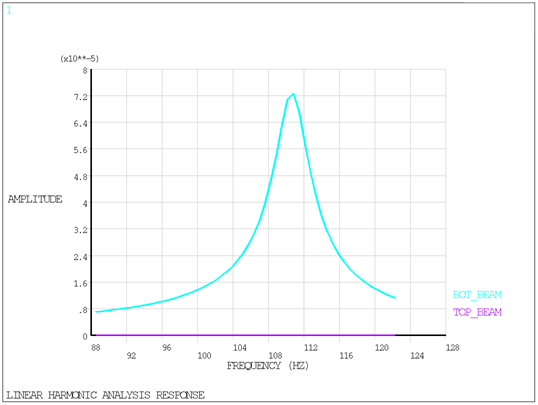
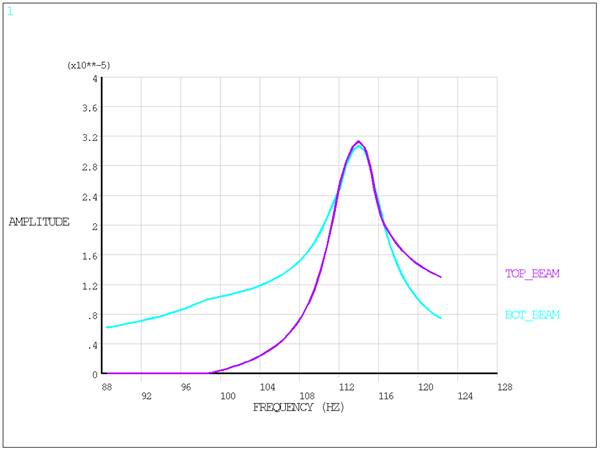
The following figure shows the linear harmonic results for the bottom beam.
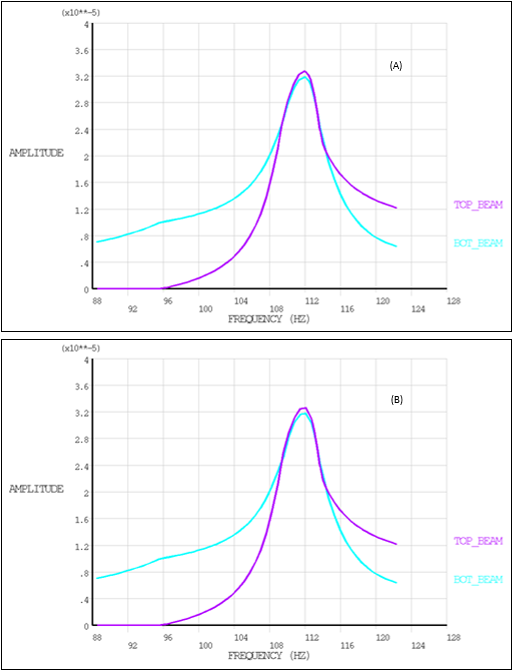
Effects of the contact on the bottom beam can be seen in the following
figure which shows a reduction in amplitude as well as an asymmetry of the peak.
Contact between the two beams occurs around 96 Hz when the top beam starts to
respond to harmonic excitation.
Compared to the full model, the CMS model gives similar results, but it reduces the overall computation time by a factor of about 6.
The prestressed CMS model also gives quite similar results. The difference lies in the localization of the peak which is shifted toward the high frequencies and the amplitude of the peak which is smaller (stiffening behavior).