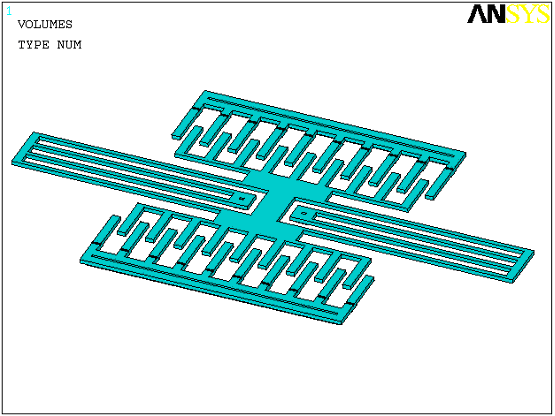
Comb drive resonators are a common application for slide film damping. Figure 5.3: Comb Drive Resonator illustrates a typical comb drive assembly consisting of fixed and moving comb drives, springs, and a central mass.
Details on the comb drive geometry are given in the input file listed below. The electrostatic behavior of the moving comb drives are represented by two TRANS126 transducer elements with prescribed Stroke vs. Capacitance data obtained from finite element runs. The structural behavior of the crab legs is modeled by a spring element. The inertial effects of the central mass are modeled with a mass element. Damping occurs between the comb teeth (lateral dimension), and between the comb teeth and the substrate (vertical dimension). Four FLUID139 elements are used to model the lateral and vertical damping (two per comb drive). The cut-off frequency is well below the frequency range for the analysis; therefore, Couette flow is assumed. Since the comb drive effective surface area changes with displacement, the DADU real constant is used (equal to the width of the plate area).
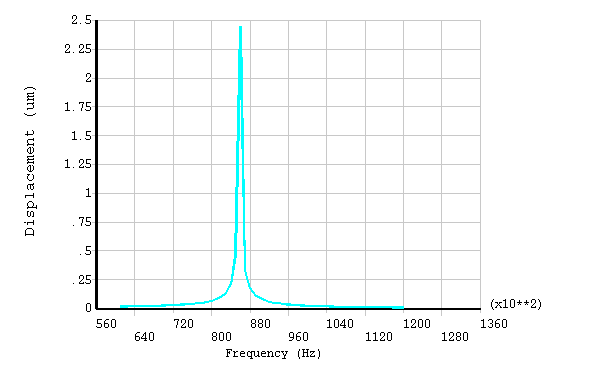
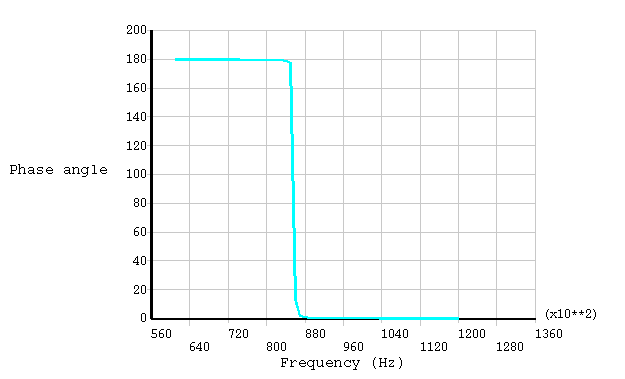
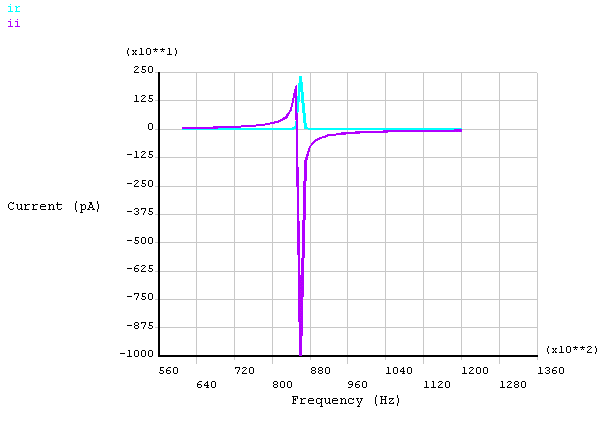
A static prestress analysis is run using a DC bias voltage on the input and output fixed comb drives. A harmonic analysis sweep is then performed using a small AC voltage. The displacement (magnitude and phase angle) of the central mass is shown in Figure 5.4: Displacement of Central Mass. Figure 5.5: Real and Imaginary Current shows the current.
/prep7 /title Comb drive resonator with FLUID139 Couette damping ! DRIVE COMB ! | ! | ! CRAB LEG SPRING --- CENTRAL MASS --- CRAB LEG SPRING ! | ! | ! PICK-UP COMB ! Reference: ! "Microelectromechanical Filters for Signal Processing", ! Lin, L., Howe, R.T., J. Microelectromechanical Systems, ! VOL 7, No. 3, Sept 1998 ! beam parameters (uMKS units) E = 190e3 !Young modulus d = 2.33e-15 ! density hb = 2 ! beam thickness wb = 2 ! beam width Lb = 100 ! beam length k = 5.699 ! mechanical stiffness ! comb parameter n= 9 ! number of finger np=n*2 ! number of finger pairs x0= 10 ! initial finger overlap L0= 26 ! finger length (stator comb) L=20 ! finger length (moving comb) gi= L0-x0 ! initial gap w= 4 ! finger width h= hb ! finger thickness gp=3 ! finger gap (lateral) g= 3 ! comb gap (vertical) Mr = 1.96563e-11 ! mass ! Lateral gap area areal=np*h*x0 ! Vertical gap area areav=n*w*x0 ! Stroke vs. Capacitance data x1 = 14 cx1 = 0.97857e-2 x2 = 15 cx2 = 0.96669e-2 x3 = 16 cx3 = 0.95445e-2 x4 = 17 cx4 = 0.94185e-2 x5 = 18 cx5 = 0.93384e-2 ! Voltage conditions Vi = 40 ! input dc bias Vo = 60 ! output dc bias Vac = 10 ! input ac bias ! Damping parmeters nu=18.3e-12 ! dynamic viscosity po=0.1 ! reference pressure dens=1.17e-18 ! density fc=nu/(2*3.14159*dens*(g**2)) ! cutoff frequency daduv=w*n ! change in plate area - vertical dadul=h*np ! change in plate area - lateral ! Model n,1,0 n,2,0 n,3,0 n,4,0 et,1,126,,0,1 !Trans126, UX-Volt DOF r,1,,,gi,, rmore,x1,cx1,x2,cx2,x3,cx3 rmore,x4,cx4,x5,cx5 e,1,2 e,2,3 et,2,21,,,4 ! Mass element r,2,Mr type,2 real,2 e,2 et,3,14,,1 ! linear spring, UX DOF r,3,k type,3 real,3 e,2,4 ! Lateral dampers et,4,139 ! Slide-film damper, Couette flow, Continuum theory mp,visc,4,nu mp,dens,4,dens r,4,g,areal,-dadul,po type,4 mat,4 real,4 e,1,2 e,2,3 ! Vertical dampers r,5,g,areav,-daduv,po real,5 e,1,2 e,2,3 d,1,ux,0 d,3,ux,0 d,4,ux,0 d,2,uy,0 d,2,volt,0 ! Prestress static analysis /solu d,1,volt,Vi d,3,volt,Vo pstres,on solve fini ! Harmonic Frequency Sweep fr0=60000 fr1=120000 /solu antyp,harm d,1,volt,Vac ! AC voltage component on capacitor d,3,volt,0 pstres,on ! prestress harfrq,fr0,fr1 nsubs,60 outres,all,all kbc,1 solve /post26 nsol,2,2,u,x,ux2 esol,3,2,,nmisc,24,ir esol,4,2,,nmisc,25,ii /axlab,x,Frequency (Hz) ! label of x axis plcplx,0 /axlab,y, Displacement (um) plvar,2 ! plot displacement versus time (frequency) plcplx,1 /axlab,y, Phase angle plvar,2 plcplx,2 /axlab,y, Current (pA) plvar,3,4 fini