This magnetic cyclic symmetry analysis uses a model of a simplified electrical machine where the model size can be reduced via cyclic boundary conditions.
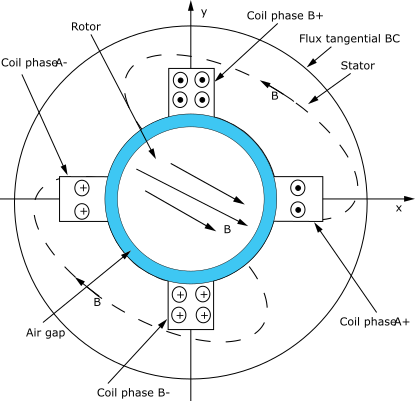
Figure 5.14: Two-Phase Electric Machine - Full Model shows a typical example, the full model of a 2-phase electrical machine.
In the full model, flux parallel boundary conditions can be formulated at the outer surface of the stator frame. If only phase A were excited, the magnetic flux would point in the y direction at x=0 plane; flux parallel condition could be formulated at the x=0 plane, allowing an analysis on a half model in the x>=0 space. Similarly, if only phase B were excited, the magnetic flux would have only x component on the y=0 plane; again, flux parallel could be applied to a half model in the y>=0 plane.
Typically, however, both coils are excited, and no flux parallel conditions could be formulated over the x=0 or y=0 planes. However, due to the cyclic nature of the field, the field pattern repeats itself after 180 degrees. In particular, on the y=0 plane:
By(x) = By(-x)
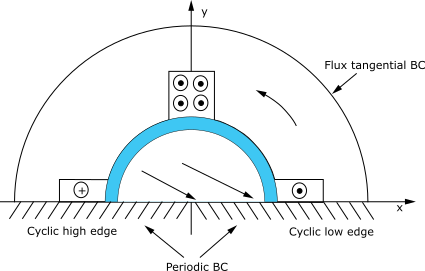
A similar pattern can be observed in Figure 5.15: Two-Phase Electric Machine - Half Model, where the flux lines (equi vector potential lines) are plotted:
Az(x) = - Az(-x)
In this example, the field has a two pole pattern. In general, there are 2p poles; the repetition would take place after 180/p degrees.
The material properties for this analysis are as follows:
Iron relative permeability: 1000
Iron electrical resistivity: 9.579E-8
Aluminum relative permeability: 1.0
Aluminum electrical resistivity: 2.65E-8
Copper relative permeability: 1.0
Copper electrical resistivity: 1.74E-8
Use this input file to perform the example magnetic cyclic symmetry analysis. This file contains the complete geometry, material properties, and solution options for the finite element model. Magnetic cyclic symmetry commands of particular interest are preceded by the comment:
!!! Apply Cylic
fini
/clear
/title,Cyclic Symmetry Model for EMAG Analysis (Dual Coils with Iron Yoke)
/com
/com ***** Quarter Symmetry Model Expanded to Half Then to Full *****
/com
/com
/com
/nopr
!!! Setup Model Parameters
p=1 ! Use for number of quarter sectors
! (i.e. 1 = 1 90deg sector, 2 = 2 sectors in 90deg)
alpha=22.5/p ! angle up to the end of first coil
beta=alpha+(45/p) ! angle from coil1 to coil2
gamma=beta+(22.5/p) ! angle from beginning of coil2 to end of sector
r1=3
r2=4.5
r3=5
r4=7
r5=11
ncoil=(4*p)
i1=1
i2=2
*dim,alpha1,,ncoil
*dim,alpha2,,ncoil
*dim,current,,ncoil
*dim,coilname,string,ncoil
coilname(1) = 'coil1'
coilname(2) = 'coil2'
coilname(3) = 'coil3'
coilname(4) = 'coil4'
*do,i,1,ncoil
alpha1(i) = -alpha + (i-1)*(90/p)
alpha2(i) = alpha + (i-1)*(90/p)
*enddo
ii=0
*do,i,1,p
ii = ii + 1
current(ii) = i2
ii = ii + 1
current(ii) = i1
ii = ii + 1
current(ii) = -i2
ii = ii + 1
current(ii) = -i1
*enddo
/prep7
ET,1,PLANE233 ! 2D magnetic element
!!! Setup Model using Parameters
PCIRC,r1, ,0,alpha,
PCIRC,r1, ,0,beta
PCIRC,r1, ,0,gamma
PCIRC,r2, ,0,alpha
PCIRC,r2, ,0,beta
PCIRC,r2, ,0,gamma
PCIRC,r3, ,0,alpha
PCIRC,r3, ,0,beta
PCIRC,r3, ,0,gamma
PCIRC,r4, ,0,alpha
PCIRC,r4, ,0,beta
PCIRC,r4, ,0,gamma
PCIRC,r5, ,0,alpha
PCIRC,r5, ,0,beta
PCIRC,r5, ,0,gamma
AOVLAP,ALL
!!! Setup Material Properties
! IRON
MP,MURX,1,1000
MP,RSVX,1,9.579E-8
! AL
MP,MURX,2,1
MP,RSVX,2,2.65E-8
! Copper
MP,MURX,3,1
MP,RSVX,3,1.74E-8
! Air
MP,MURX,4,1
MP,RSVX,4,0
!!! Setup Components and Atributes
! Iron Core
CSYS,1 ! Enter Cylindrical Mode
ASEL,S,LOC,X,0,r1
CM,Inner_Iron,AREA
AATT,1,,1,
! Al Core
ASEL,S,LOC,X,r1,r2
CM,Outer_AL,AREA
AATT,2,,1,
! Air Gap
ASEL,S,LOC,X,r2,r3
CM,AIR,AREA
AATT,4,,1
! Coil 1
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,0,alpha
CM,COIL1,AREA
AATT,3,,1
! Coil 2
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,beta,gamma
CM,COIL2,AREA
AATT,3,,1
! Iron Yoke
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,alpha,beta
ASEL,A,LOC,X,r4,r5
CM,YOKE,AREA
AATT,1,,1
ALLSEL
CSYS,0 ! Enter Cartesian Mode
!!! Setup and Mesh Model
MSHKEY,1
CSYS,1
LSEL,S,LOC,Y,0
LSEL,A,LOC,Y,gamma
LESIZE,ALL,,,6,,1,,,1,
CMSEL,S,Inner_Iron
AMESH,ALL
CMSEL,S,Outer_AL
AMESH,ALL
CMSEL,S,Air
AMESH,ALL
CMSEL,S,Coil1
AMESH,ALL
CMSEL,S,Coil2
AMESH,ALL
CMSEL,S,Yoke
AMESH,ALL
ALLSEL
CSYS,0
!!! Reflect Model across X-axis
!! Create HALF model from QUARTER model
arsym,x,all
/prep7
save,magtest,db ! save half model for cyclic
arsym,y,all ! create full model reflecting on y axis
nummrg,all
csys,1
nsel,s,loc,x,r5
CM,extnode,NODE
! Apply BFE Current loads to each coil
*do,i,1,ncoil
asel,s,loc,x,r3,r4
asel,r,loc,y,alpha1(i),alpha2(i)
esla,s
cm,coilname(i),element
bfe,all,js,,,,current(i)
*enddo
csys,0
allsel
cmsel,s,extnode
d,all,az,0
allsel
FINISH
/solu
antype,static
allsel
solve
FINISH
/post1
!!! Plot Out Result Plots
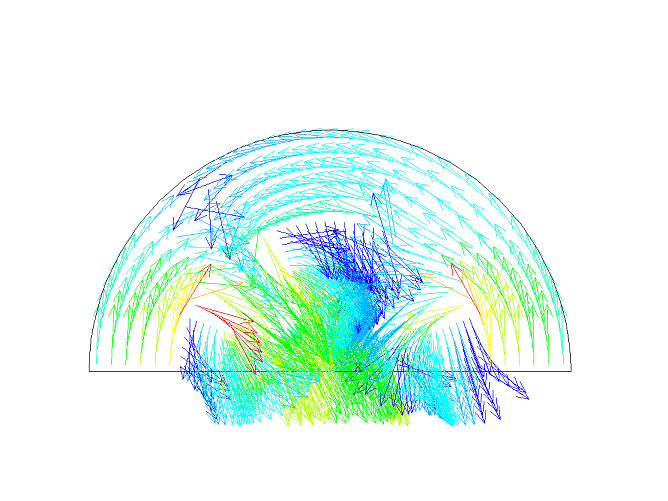
plvect,b,,,,VECT,ELEM,ON,0
FINISH
parsav,all
/clear,nostart
resume,magtest,db ! Resume half Model
parres,new
!! Delete Bottom half of model and all loading attatched to bottom nodes
/prep7
allsel
nummrg,all
csys,1
nsel,s,loc,x,r5
d,all,az,0 ! AZ = 0 on outside nodes of arc
!! Define Coils on Half Model
! Coil 1
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,0,alpha
esla,s
CM,COIL1,ELEMENT
! Coil 2
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,beta,(180-beta)
esla,s
CM,COIL2,ELEMENT
! Coil 3
ASEL,S,LOC,X,r3,r4
ASEL,R,LOC,Y,(180-alpha),180
esla,s
CM,COIL3,ELEMENT
!! Apply bfe loads to Half Model coils
cmsel,s,COIL1
bfe,all,js,,,,i2
cmsel,s,COIL2
bfe,all,js,,,,i1
cmsel,s,COIL3
bfe,all,js,,,,(-i2)
!!! Apply cyclic - create cyclic model with two sectors
allsel
csys,0
cyclic,2
/solu
cycopt,hindex,odd ! Odd Symmetry for half model
solve
FINISH
/post1
/vscale,1,1,1
plvect,b,,,,VECT,ELEM,ON,0 ! B field
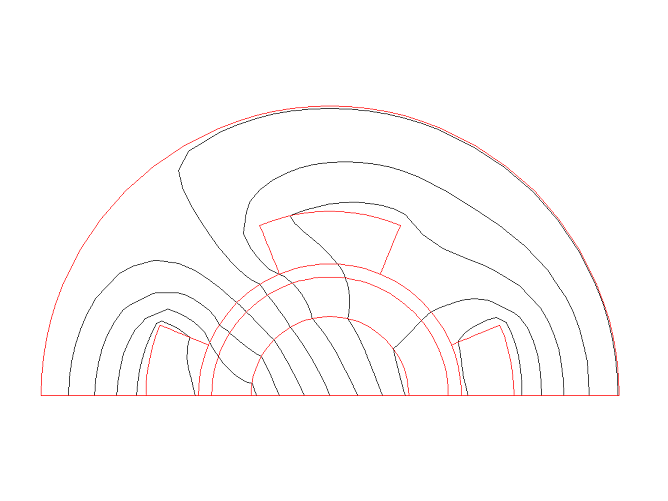
plf2d ! Equipotential lines
FINISH