The model uses the Drucker-Prager yield criterion with either an associated or nonassociated flow rule. The yield surface does not change with progressive yielding; therefore, there is no hardening rule and the material is elastic-perfectly plastic (Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options (f) Drucker-Prager). The equivalent stress for Drucker-Prager is:

(5–1)

where:

{s} = deviatoric stress Equation 4–37

β = material constant

[M] = as defined with Equation 4–36

This is a modification of the von Mises yield criterion (Equation 4–36 with {α} = {0}) that accounts for the influence of the hydrostatic stress component: the higher the hydrostatic stress (confinement pressure) the higher the yield strength. β is a material constant which is given as:

(5–2)

where:

The material yield parameter is defined as:

(5–3)

where:

The yield criterion Equation 4–7 is then:

(5–4)

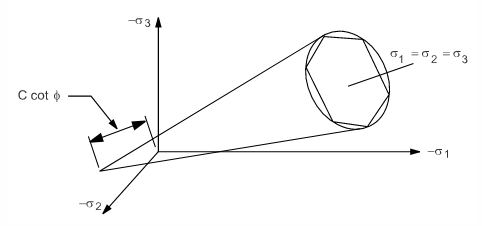
This yield surface is a circular cone (Figure 4.2: Various Yield Surfaces-c) with the material parameters Equation 5–2 and Equation 5–3 chosen such that it corresponds to the outer aspices of the hexagonal Mohr-Coulomb yield surface:

Figure 5.1: Drucker-Prager and Mohr-Coulomb Yield Surfaces

is readily calculated as:

(5–5)

is similar, however β is evaluated using φ_f (the input dilatancy constant). When φ_f = φ, the flow rule is associated and plastic straining occurs normal to the yield surface and there will be a volumetric expansion of the material with plastic strains. If φ_f is less than φ there will be less volumetric expansion and if φ_f is zero, there will be no volumetric expansion.

The equivalent plastic strain (output as EPEQ) is defined by Equation 4–43 and the equivalent stress parameter (output as SEPL) is defined as:

(5–6)

The equivalent stress parameter is interpreted as the von Mises equivalent stress at yield at the current hydrostatic stress level. Therefore, for any integration point undergoing yielding (stress ratio (output as SRAT) >1), should be close to the actual von Mises equivalent stress (output as SIGE) at the converged solution.