This example problem demonstrates the use of the FLUID220 element to predict the transmission loss of an infinite structural panel under excitation from an obliquely incident plane wave. The Floquet periodic boundary condition is used to truncate the infinite panel.
The material properties of the structural panel with thickness 0.0508 m are:
| Elastic moduli = 206.84 GPa |
| Minor Poisson's ratios = 0.3 |
| Mass density = 7500 kg/m3 |
The acoustic domain is the water with mass density = 1000 kg/m3 and sound speed = 1498.6 m/s.
FSI between the acoustic incident wave and the structural panel is taken into account.
Excitation and output plane wave ports are defined on the interior surfaces.
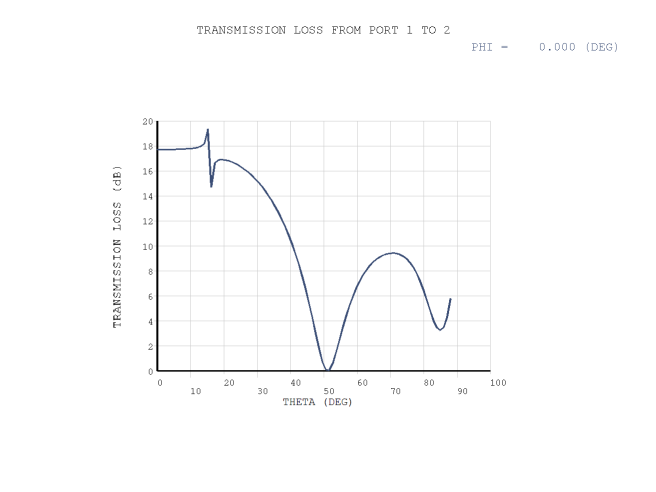
The incident angle θ (from +z axis toward +x axis) sweeps from 0° to 88° at the φ = 0° plane.
The Floquet periodic boundary condition is applied on the cell sidewalls in the x-direction.
The program calculates the phase shift on the dependent nodes according to the incident angles.
Perfectly matched layers (PML) truncate the domain in the z-direction. For more information, see Perfectly Matched Layers (PML) in the Mechanical APDL Theory Reference.
/batch, list /nopr /prep7 et,1,220,, ! coupled acoustic element et,2,220,,1,,1 ! acoustic PML element et,3,186 ! structural element rho1 = 1000 ! acoustic fluid mass density c01 =1498.6 ! sound speed in acoustic fluid rho2 = 7500 ! structural mass density ex=2.0684e11 ! structural Young's module nuxy=0.3 ! poison ratio freq = 10000 ! working frequency wavelen = c01/freq ! wave length dL=0.0508 ! period dd=1.0*wavelen dpml=0.5*wavelen ! PML thickness h=wavelen/32 ! mesh size p0=1 ! amplitude of incident pressure wave mp,dens,1,rho1 ! define acoustics material mp,sonc,1,c01 mp,dens,2,rho2 ! define structural material mp,ex,2,ex mp,nuxy,2,nuxy *dim,c,array,6 ! set up geometry c(1)=0 c(2)=c(1)+dpml c(3)=c(2)+dd c(4)=c(3)+dL c(5)=c(4)+dd c(6)=c(5)+dpml *do,i,1,5 block,-dL/2,dL/2,-h,h,c(i),c(i+1) *enddo vglue,all vsel,s,loc,z,c(3),c(4) ! generate mesh type,3 mat,2 esize,h vmesh,all vsel,s,loc,z,c(2),c(3) vsel,a,loc,z,c(4),c(5) type,1 mat,1 vmesh,all vsel,s,loc,z,c(1),c(2) vsel,a,loc,z,c(5),c(6) type,2 mat,1 vmesh,all alls nsel,s,loc,z,c(3) ! flag FSI interface nsel,a,loc,z,c(4) sf,all,fsi nsel,s,loc,x,-dL/2 ! coupled nodes nsel,a,loc,x,dL/2 nsel,r,loc,z,c(1),c(6) cpcyc,all,,,dL nsel,s,loc,z,c(5) ! define plane wave excitation at port 1 bf,all,port,1 aport,1,plan,0,p0 nsel,s,loc,z,c(2) ! define output port at port 2 bf,all,port,2 aport,2,plan nsel,s,loc,z,c(1) ! pml exterior b.c nsel,a,loc,z,c(6) d,all,pres,0 alls d,all,uy,0 ecpchg fini /solu ! perform solution eqslv,sparse pmlopt,,,,,,,1.e-7,1.e-7 antype,harmic hropt,auto harfrq,freq nsub,1 msolve,88,0,88,aphi,0 ! angle theta sweep with fixed phi=0 fini /post1 /show,png pras,tl,all,1,,,,,1,2 ! print transmission loss plas,tl,all,1,,,,,1,2 ! plot transmission loss fini
The transmission loss of the structural panel under an obliquely incident plane wave is shown in this figure: