This example uses FLUID220 elements to demonstrate the simulation of sound characteristics in a one-dimensional domain with the length L by solving the transient Westervelt equation [1].
The initial boundary conditions are:
and
for
A pulse source is located at and given by:
where is the pressure amplitude,
is the frequency of the source,
is a time delay,
is a pulse width and
is the end of the pulse.
is the Heaviside step function. The pulse parameters are set to
,
, and
.
The fluid material is water with a mass density = 999.6 kg/m3 and speed of sound
= 1481.44 m/s. Water typically has a dimensionless nonlinearity
coefficient
of about 3.5. In this example, setting
= 10 shortens the shock wave distance by about a factor of 3 to speed
up the computation. The shock wave distance is defined as:
The domain length is set to to ensure the pulse travels 95% of the shock wave distance. The
element size is
and the time step is
.
/batch
/nopr
/prep7
! water property
pi=acos(-1)
rho0=999.6
c0=1481.44
beta=10
! pulse parameters
P0=1e6
f0=1e5
Td=6/f0
Tw=3/f0
Tend=12/f0
! computational parameters
xsh=rho0*c0**3/(beta*P0*2*pi*f0)
L=0.95*xsh+Tend*c0
dx=c0/18/f0
dt=dx/20/c0
! define element type solving Westervelt equation
et,1,220,,9
! define model material
mp,dens,1,rho0
mp,sonc,1,c0
tb,afdm,1,,,mat
tbfield,time,0
tbdata,1,rho0,c0,0,0,0,0
tbdata,7,0,0.0,beta
! FEM domain
block,0,dx,0,dx,0,L
esize,dx
type,1
mat,1
vsel,s,loc,z,0,L
vmesh,all
alls
! pulse source
Nt=NINT(Tend/dt)+1
*dim,_pp,TABLE,Nt,1,1,TIME
*do,i,0,Nt
_pp(i,0,1)=i*dt
tt=i*dt
*if,_pp(i,0,1),lt,Tend, then
pt=P0*sin(2.*pi*f0*(tt-Td))*exp(-4*(tt-Td)**2/Tw**2)
_pp(i,1,1)=pt
*else
_pp(i,1,1)=0.0
*endif
*enddo
nsel,s,loc,z,0
d,all,pres,%_pp%
alls
fini
/solu
eqslv,sparse
antype,trans
rescontrol,define,all,all
outres,all,all
time,0.45e-3
deltim,dt
solve
fini
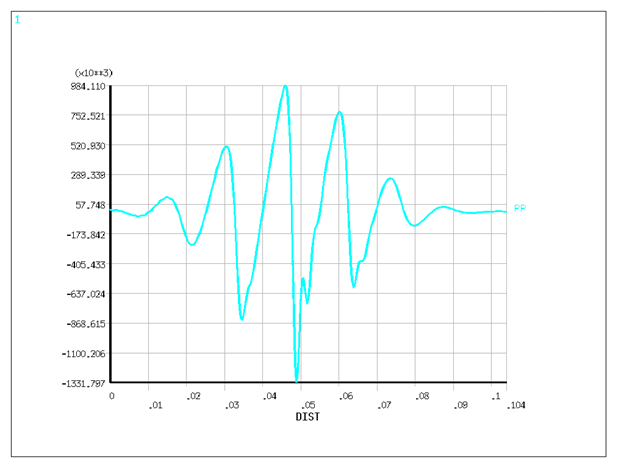
/post1
xsh=0.52
SET,,,1,,0.443e-3,
FLST,2,2,1
FITEM,2,node(0,0,xsh)
FITEM,2,node(0,0,xsh*1.2)
PATH,w15,2,500,300,
PPATH,P51X,1
PATH,STAT
AVPRIN,0, ,
PDEF,pp,pres
/PBC,PATH, ,0
/show,png
PLPATH,pp
/show,close
Fini