Two different parametrizations of the Hill yield criterion with respect to the principal values of the orientation tensor are available:
Following [Launay 2013], we adopt the following phenomenological parametrization of the Hill yield criterion:
(3–65) |
where
denotes the i-th eigenvalue of the second order fiber orientation tensor
is a parameter describing the sensitivity of the yield criterion to the orientation distribution
is a regularization parameter.
Note that the regularization term was not present in the original model by
[Launay
2013], in which case no plastic flow can develop along the fiber
direction of a unidirectionally aligned composite– that is,
for
. Since this assumption does not hold for short fiber
reinforced composites, the term
is added here, where the constant
(3–66) |
depends on the volume fraction and the aspect ratio
of the fibers.
The directional yield ratios then read
(3–67) |
Some comments are in order:
The yield ratios in shear direction are independent of the fiber orientation.
For
, which is in the limit of high fiber volume fraction and/or high fiber aspect ratio, the expression for the yield ratios in normal direction reduces to the original one in [Launay 2013]. See the figure below.
For
, it reduces to the von Mises Yield criterion.
For a generic
and a completely random fiber orientation distribution
up to a scaling factor, it reduces to the von Mises criterion in the limit of
.
Figure 3.2: Effect of the aspect ratio, fiber volume fraction, and orientation sensitivity parameter on the yield ratio in normal direction
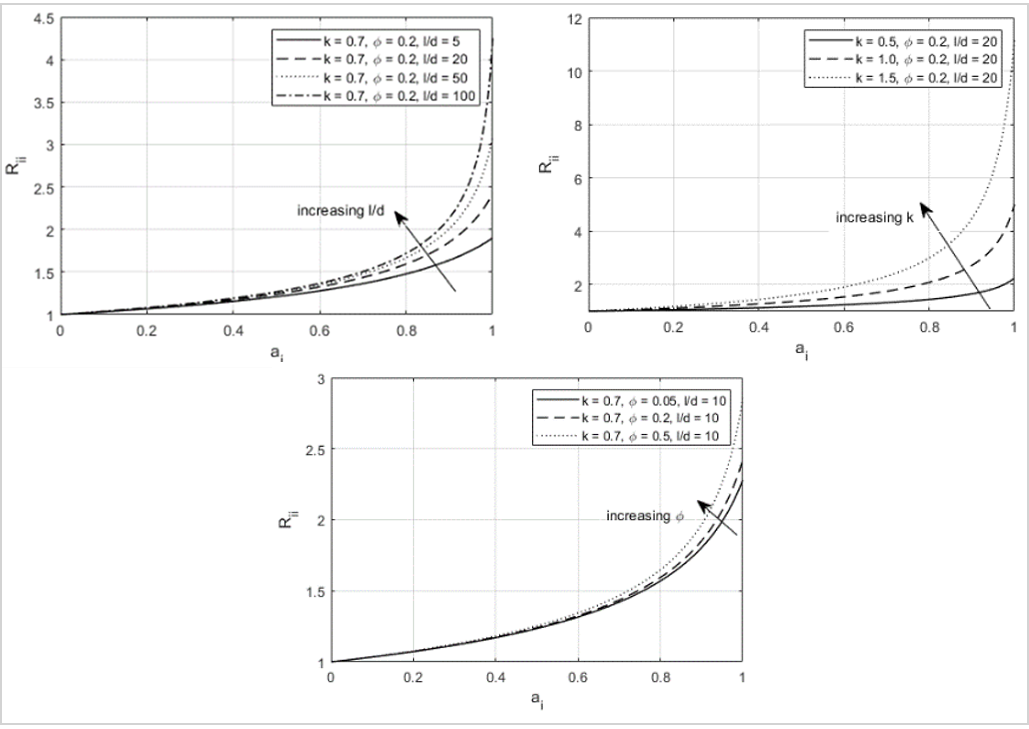
Assume that the Hill yield strength of a unidirectional short fiber composite is known. To predict the strength of a composite with arbitrary fiber orientations, we can follow an approach similar to that used for the homogenization of linear elastic properties.
Let denote the Hill strength tensor of a unidirectional
composite with inclusions aligned along the direction
. Following [Van Hattum et al., 1999], we rewrite the yield criterion (Equation 3–59 to Equation 3–61) in strain
space:
(3–68) |
where and
is the stiffness tensor of the unidirectional composite.
The strength properties of a composite with arbitrary fiber orientations are
computed as an average of unidirectional composite properties over all
directions, weighted by the orientation distribution function
(3–69) |
The tensor admits the same representation as in Equation 3–5 and can be easily
computed in terms of the second and fourth-order fiber orientation tensors.
The final orientation averaged yield strength tensor (in stress form) is
obtained as
(3–70) |
This procedure relies on the assumption of knowing
the strength of the unidirectional composite. In such case, the Hill yield
tensor is transversely isotropic and only depends on three
independent parameters: the yield stress in the longitudinal and transverse
directions (
and
, respectively), and the longitudinal shear stress
. For instance, for a unidirectional composite with fibers
aligned along the material 1 direction, the yield stresses in Equation 3–64 are given by
|
|
The values of ,
, and
can be, for instance, predicted from micro-mechanical
considerations (see for example [Van Hattum
et al., 1999]. In Material Designer, they are reverse-engineered from
experimental stress-strain curves as described in Hill Yield Criterion.


