Determining Phase Center Using Optimetrics
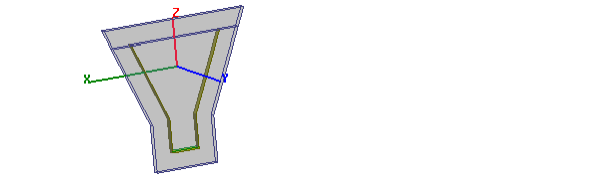
The phase center is the point from which the electromagnetic radiation spreads spherically outward, with the phase of the signal being equal at any point on the sphere. This example illustrates a technique for using an optimization setup to search for the phase center.
The technique involves the following tasks.
This allows the variable value to change the definition of the coordinate system and thereby change a solved solution without invalidating it.
- Use a relative coordinate system in a Far field setup calculation.
This allows far field quantities to be re-calculated when the relative coordinate system is repositioned (demonstrated in the example by changing the value of the PhaseCenterZ variable), without re-simulation.
The far field setup will also limit the angular range of the sweeping intrinsic (phi or theta).
- Create an optimization setup to search for the phase center. The search will be efficient if you have a rough idea on the location of the phase center. The expression to be optimized is the peak to peak continuous angle of the quantity rEPhi. (The electric field of this antenna is Phi polarized.)
- Analyze the Optimization setup and view results via the View Analysis Result dialog.
The Z coordinate of the phase center will be the value of the post processing variable when Cost is at minimum.

The following sections detail these steps for setting up an Optimetrics project to calculate the Phase Center.
