If the flow is nonisothermal, the temperature dependence of the viscosity must be taken into account along with the shear-rate dependence. The viscosity law can be factorized as follows:
(10–17) |
where is the Arrhenius law (or one of the other available laws) and
is the viscosity law at some reference temperature
(as computed by one of the shear-rate-dependent laws described
above).
The Arrhenius law is given as
(10–18) |
where is the ratio of the activation energy to the thermodynamic
constant, and
is a reference temperature for which
. The temperature shift
is set to 0 by default, and corresponds to the lowest
temperature that is thermodynamically acceptable. Therefore
and
are absolute temperatures. They can also be defined relative
to a non-absolute temperature scale, in which case
corresponds to the absolute zero temperature in the current
temperature scale.
Two versions of the Arrhenius law are available: one based on shear rate and one based on shear stress, as described below. Both methods provide similar, although not identical, results for most polymers.
Not all polymers strictly follow Equation 10–17. While this requires detailed measurements of the viscosity as a function of the temperature, most polymers follow a viscosity-temperature dependence that is slightly different from Equation 10–17.
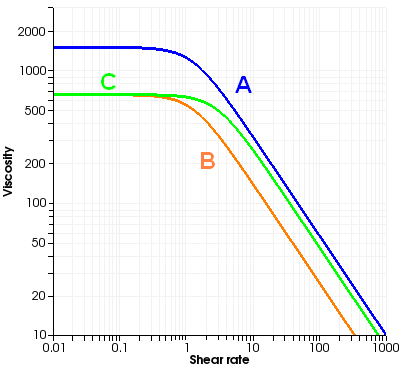
Consider a typical viscosity curve such as the one shown in Figure 10.1: Typical Viscosity Curve. Curve A
represents the viscosity at a reference temperature, say . This viscosity curve, which has been modeled using a
Bird-Carreau law, presents a plateau zone for low shear rates.
If the polymer were to follow Equation 10–17, curve A would translate at a different temperature, say 200°, into curve B. This is the behavior modeled with either the Arrhenius or the approximate Arrhenius laws. However, sometimes the viscosity at 200° follows curve C; that is, not only is the absolute value of the viscosity decreased, but also the point of departure from the constant-viscosity regime moves toward the right in the diagram. This is precisely what the "shear stress" version of the temperature-dependence laws models, using the following equation:
(10–19) |
where the shear-rate dependence of the viscosity is now given as a function of
instead of
only.
The law of Equation 10–19 corresponds to a vertical shift of the viscosity curve in a viscosity-shear-stress diagram, so it is referred to as the Arrhenius shear-stress law.
Note that a power-law model does not reflect the difference between Arrhenius shear rate and Arrhenius shear stress because of the absence of a transition zone.
The approximate Arrhenius law is written as follows:
(10–20) |
The behavior described by Equation 10–20 is similar to that described by Equation 10–18 in the
neighborhood of . Equation 10–20 is valid as long as the temperature difference
is not too large. As for the Arrhenius law, two versions are
available: one based on shear rate and one based on shear stress, as described
above.
Another definition for comes from the Fulcher law [14]:
(10–21) |
where ,
, and
are the Fulcher constants. The Fulcher law is used mainly for
glass.
As can be seen, Equation 10–21 leads to a
significant viscosity increase of when the temperature decreases, until it reaches the value
T=
, where
then exhibits a singularity. Unbounded values are not so
desirable for the solver. Hence, the factor
has been purposely bounded to
or to slightly higher values when too small a value is
selected for the parameter
. This bound has been introduced in such a way that the
function and its derivatives are continuous.
The Williams-Landel-Ferry (WLF) equation is a temperature-dependent viscosity law that fits experimental data better than the Arrhenius law for a wide range of temperatures, especially close to the glass transition temperature:
(10–22) |
where and
are the WLF constants, and
and
are reference temperatures.
The WLF law described above is based on shear rate. As for the Arrhenius law,
there is also a version of the WLF law based on shear stress. In this version,
the viscosity is computed from Equation 10–19,
with
computed from the WLF law, Equation 10–22. As for the Arrhenius shear-stress law, an increase
in temperature will result in a shifting of the viscosity curve downward and to
the right.
For the mixed-dependence law (which can be used only in conjunction with the
log-log law for shear-rate dependence), the function is written as
(10–23) |
where is computed from the log-log law (Equation 10–15) and
(10–24) |
In this equation, ,
, and
are the coefficients of the polynomial expression, and
is the lowest temperature that is thermodynamically
acceptable, with respect to the current temperature scale. Typically, if the
units for temperature are Kelvin,
will be 0; if the units for temperature are Celsius,
will be –273.15.