Eigenvalue Analysis can be used to calculate the eigenvalue and eigenvector, or the frequency response of a system. The mass and stiffness of the system are considered and the damping matrix is ignored during this analysis as in the following equations.
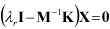 | (9–13) |
 | (9–14) |
 | (9–15) |
where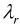 
is the eigenvalue and Ψ
is the eigenvector (mode shape). The stiffness matrix 
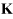can be calculated from the partial derivative
of the equation of motion for the generalized coordinate. The reported natural
frequency in Hz can be calculated from the following equation.
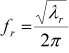 | (9–16) |
Remarks
If the system has a nodal flexible body or nodal EasyFlex body, the Motion solver will require a huge amount of memory and the analysis may fail due to memory shortage. If this is the case, the analysis can be completed successfully by changing the body to a modal flexible body. It is possible to model a modal flexible body with body eigenvalue analysis.
The Motion solver creates a dummy body with a very small mass at the master point location of a RBE (Rigid Body Element). The mass of this dummy body is automatically determined by the solver. While this dummy body generally does not significantly affect the solution, it can influence the outcome under certain conditions, such as when the number of nodes on a flexible body is less than 1000 or if the master node of the RBE is located relatively far from the structure. If the natural frequency appears lower than expected after an eigenvalue analysis, setting the
dummymasstpto1in the the solver commands can resolve this issue by further reducing the mass of the dummy body.