VM-WB-MECH-068
VM-WB-MECH-068
Plastic Loading of a Thick Walled Cylinder
Test Case
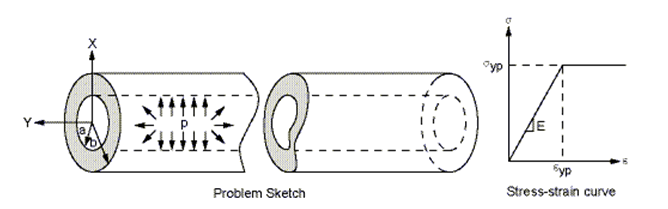
A long thick-walled cylinder is subjected
to an internal pressure p (with no end cap load). Determine the radial
stress, σr, and the tangential (hoop)
stress, σt, at locations near the inner
and outer surfaces of the cylinder for a pressure, pel, just below the yield strength of the material, a fully elastic
material condition. Determine the effective (von Mises) stress, σeff, at the same locations for a pressure, pult, which brings the entire cylinder wall into a state
of plastic flow. Use a global mesh size of 0.4 in along with a mapped
face meshing.
Analysis
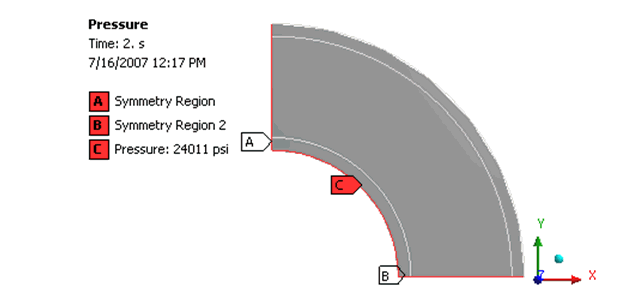
This problem is modeled as a plane strain problem with only
a quarter of the cross-section as shown in the above figures. Symmetry
conditions are used on the edges perpendicular to X and Y axes. Load
is applied in two steps as shown in the above table. The stresses
are calculated at a distance of r = 4.4 in and 7.6 in, w.r.t a cylindrical
coordinate system whose origin is same as that of the global coordinate
system.