19.11.3.1. Fatigue Material Properties for Random Vibration (Spectral) Fatigue

All Frequency-Based Fatigue formulations are driven by the material’s relationship between Stress (S) and number of life cycles (N). This S-N relation can be defined in the Engineering Data Workspace using any of the following:

Important:

  • For Frequency-Based Fatigue calculations, you need to employ at least one of the SN Curve formulations listed above in order to proceed with a solution.

  • For both the Linear S-N Curve and the Bi-linear S-N Curve, the reference units for the parameters is [Pa]. No other unit or unit system is currently supported.

  • In the various S-N Curve formulas covered here, the "S" value always refers to Stress Amplitude.

As long as you define material properties using one of the above formulas, you can perform Frequency-Based Fatigue calculations.

Linear S-N Curve Formula

This is a single segment S-N Curve formula of the form:

Where:

A = Fatigue Strength Coefficient
m = Fatigue Strength Exponent
S = Stress Amplitude (in Pa)

Note:  The value "m" is the inverse negative slope of the Linear S-N Curve.

Bi-Linear S-N Curve Formula

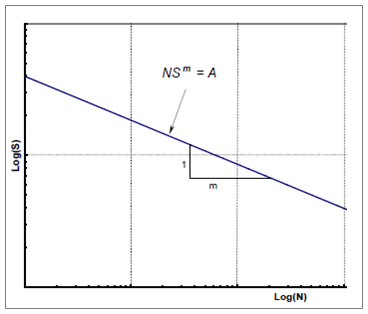
This is a two segment S-N Curve formula of the form:

&

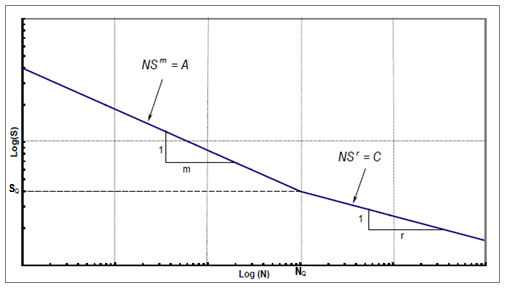
Where:

A = First Fatigue Strength Coefficient
m = First Fatigue Strength Exponent
C = Second Fatigue Strength Coefficient
r = Second Fatigue Strength Exponent
SQ = Stress Amplitude at Transition Point (in Pa)
NQ = Number of cycles at Transition Point

Using the Derive from property in Engineering Data Workspace, select one of two methods of definition:

  • Coefficients and Exponents: Users define A, m, C, and r.

  • Transition Point: define m, r, NQ, and SQ.

All other properties are automatically calculated.

Note:  The "m" and "r" values are the inverse negative slopes of the Bilinear S-N Curve.

S-N Curve Table

As illustrated below the default data for the S-N Curve is contained in the Engineering Data Workspace tabular data of corresponding Alternating Stresses and Cycles of life.

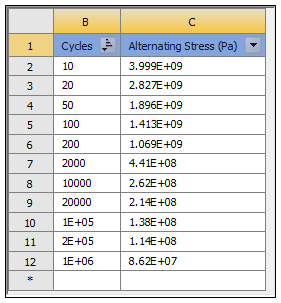
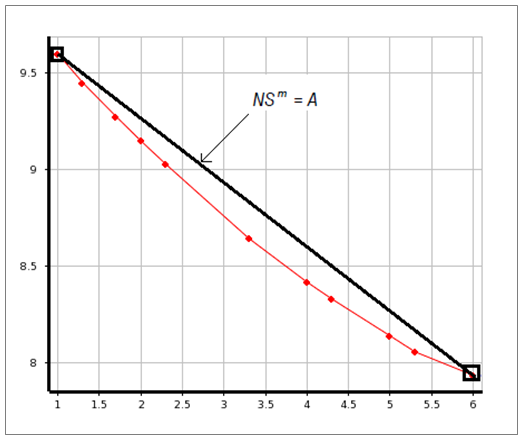
Note:  If only the SN table is provided (and not the Linear/Bilinear parameters themselves), then the solver will use the first and last points of the table to perform a linear interpolation using equation and arrive at the required parameters of A and m. Once the A and m values are obtained, we can proceed with the solution normally. If either of the parameters (Linear/Bilinear) are provided directly through the material definition, they will be used directly. (The table, if present, will be ignored in this case).