The proper selection of a fluid model is one of the most important aspects in the simulation of a flow. You need to always consider both the fluid and the flow; a particular constitutive equation is valid for a given fluid in a given flow.
To determine an appropriate model for your problem, you need to first collect as much data as possible about the fluid properties. Typical information includes the following:
Steady viscometric properties (shear viscosity
and first normal-stress difference
). These data characterize the fluid in the presence of large deformations.
Oscillatory viscometric properties (storage and loss moduli
and
), also known as linear viscoelastic data because they correspond to small deformations.
Elongational viscosity. Although obtaining data on elongation is difficult and not very frequent, knowledge of the elongational viscosity is essential in choosing the appropriate constitutive equation and estimating the values of the various parameters.
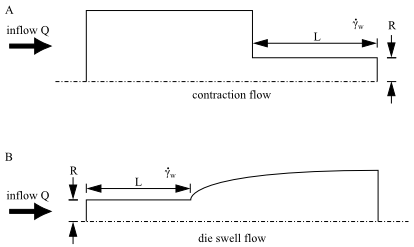
These data are not enough to evaluate the relevance of viscoelasticity in a given process. It is also necessary to characterize the flow itself and compare a characteristic time of the material to a characteristic time of the flow. In many situations, the flow can be characterized by a critical shear rate, which can be understood as a wall shear rate in a region of high gradients. For example, in a fiber-spinning process, a critical shear rate will occur at the wall in the vicinity of the die exit. In a contraction or expansion flow (for example, Figure 6.1: Contraction and Expansion Flow), consider the shear rate in the narrow section.
In a planar flow (Figure 6.1: Contraction and Expansion Flow a),
(6–1) |
where is a typical distance.
In an axisymmetric flow (Figure 6.1: Contraction and Expansion Flow b),
(6–2) |
where is a typical radius.
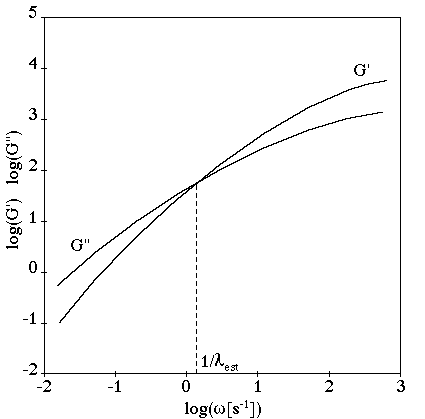
You also need to determine the elastic level of the fluid. This can be accomplished by
evaluation of the fluid’s characteristic relaxation time. When the oscillatory
functions and
are available, their intersection (occurring at a shear rate
, as shown in Figure 6.2: Storage and Loss Moduli Curves) is often a reasonable choice for selecting a typical
relaxation time. Indeed, flows characterized by a typical shear rate lower than
are essentially dominated by viscous forces, while viscoelastic
effects may play an important role in flows characterized by a shear rate higher than
.
Note that, due to the technological limitations of some rheometry equipment, it is not always possible to obtain viscoelastic data in the range of shear rates (or angular frequencies) where the process operates. In this case, your only option is to extrapolate experimental data for higher shear rates or angular frequencies. The selection of a particular model for such a case will be more qualitative.
A typical dimensionless number used to estimate the viscoelastic character of a flow
is the Weissenberg number , which is the product of the relaxation time
and a typical shear rate
:
(6–3) |
When is low, generalized Newtonian models are sufficient to describe the
flow; only at higher values of
are viscoelastic models required to characterize memory effects.
Note that the Weissenberg number is probably not the best indicator for viscoelastic
models with several relaxation times or if there is shear thinning in the flow. In such
cases, a useful dimensionless number is the recoverable shear , defined as the ratio of the first normal-stress difference
to twice the steady shear stress
:
(6–4) |
The recoverable shear gives the level of elasticity of a flow: if
>1, the viscoelastic character of the flow is important, and a
viscoelastic model is required.