There are two integral viscoelastic models provided in Ansys Polymat:
Doi-Edwards model: Theoretically, this model has an infinity of relaxation times, determined by only two parameters: the main relaxation time and the zero-shear-rate viscosity. This constitutive equation is characterized by shear thinning and a non-quadratic first normal-stress difference at high shear rates. It also predicts a nonzero second normal-stress difference and a finite steady extensional viscosity.
For stability reasons, however, it is necessary to add a purely viscous component to the extra-stress tensor for simple shear flows. The viscosity associated with this purely viscous stress leads to a plateau zone at high shear rates. In this way, the slope of the curve
as a function of
is greater than
.
KBKZ model: In addition to the spectrum that describes the linear viscoelastic behavior of the material, the KBKZ model also makes use of a damping function. The damping function can be a constant value, or one of two functions: Papanastasiou-Scriven-Macosko (PSM) or Wagner. Each of these two functions has a reversible and an irreversible function type. Both functions are controlled by two parameters:
and
for the PSM model and
and
for the Wagner model. A third parameter,
, affects the ratio of the second to the first normal-stress difference.
For the PSM model, high values of
lead to a large constant viscosity plateau;
corresponds to a constant damping function, which corresponds to a Lodge-Maxwell model. If
decreases, the constant viscosity plateau moves toward lower shear rates. For the Wagner model, high values of
lead to a short constant viscosity plateau, while a small value of
gives a plateau for a large range of shear rates.
For small values of the invariant
(a combination of
and
, defined in Equation 6–80), both damping functions are very similar. For high values of
, however, the exponential function of the Wagner model decreases more quickly than the rational function of the PSM model. High values of
occur in the case of large deformations.
The
parameter has no effect on the shear viscosity or on the first and second normal-stress differences. It affects only the extensional viscosity. A zero value for
leads to an unbounded steady extensional viscosity. Increasing
decreases the maximum value of the steady extensional viscosity curve.
For the PSM and Wagner models, it is possible to introduce the concept of irreversibility originally mentioned by Wagner [12]. The idea is that the damping function must only decrease. According to Wagner, this is a realistic assumption when intermolecular association occurs, as in a narrowing part of a duct, for example. In the case of a high flow rate through a contraction followed by an expansion, it is reasonable not to allow the damping function to increase again after the narrowing of the channel.
As for the Doi-Edwards model, it is necessary to add a purely viscous component to the extra-stress tensor for simple shear flows with the KBKZ model.
Details about each model are provided below.
The Doi-Edwards model is characterized by shear thinning and a non-quadratic first normal-stress difference at high shear rates. It also predicts a non-vanishing second normal-stress difference and a finite steady extensional viscosity.
In the Doi-Edwards model, is computed from
(6–73) |
where
(6–74) |
and
(6–75) |
In Equation 6–73,
is the index of the relaxation mode.
(optional, but strongly recommended) is computed from Equation 6–27.
The KBKZ model provides additional accuracy by including a damping function
in its constitutive equations. is computed from
(6–76) |
and (optional, but strongly recommended) is computed from Equation 6–27, based on
the specified value of
.
In Equation 6–76,
is the index of the relaxation mode and
is a scalar parameter that controls the ratio of the
normal-stress differences:
(6–77) |
and is the damping function. The simplest case (Lodge-Maxwell
model) is for no damping:
and
.
The Papanastasiou-Scriven-Macosko (PSM) model computes from
(6–78) |
where is a material parameter that primarily influences the
shear-thinning behavior. The default value for
is 1, which may be unrealistic for many fluids, due to the
large possible range of this parameter.
The Wagner model
computes from
(6–79) |
where is a material parameter that influences both the shear
viscosity and the elongational behavior of the material.
The reversible PSM model uses Equation 6–78,
allowing to increase or decrease. The irreversible PSM model allows
only to decrease.
Similarly, the reversible Wagner model uses Equation 6–79,
allowing to increase or decrease. The irreversible Wagner model allows
only to decrease.
In both Equation 6–78 and Equation 6–79,
is computed from
(6–80) |
where and
are given by Equation 6–69 and Equation 6–70.
is a material parameter that influences only the elongational
behavior of the material. The default value for
is 1, which may be unrealistic for many fluids, due to the
large possible range of this parameter.
Figure 6.60: Storage and Loss Moduli for Oscillatory Shear Flow through Figure 6.70: Comparison of Reversible and Irreversible PSM Damping Functions for Transient Shear Flow (α=14.38) show the influence of each parameter of the damping models on the rheological curves for a low-density polyethylene with the following parameters:
|
|
|
|
| 1 | 12.9 | 10–4 |
| 2 | 94.8 | 10–3 |
| 3 | 586.0 | 10–2 |
| 4 | 2670.0 | 10–1 |
| 5 | 9800.0 | 10+0 |
| 6 | 18900.0 | 10+1 |
| 7 | 18000.0 | 10+2 |
| 8 | 1000.0 | 10+3 |
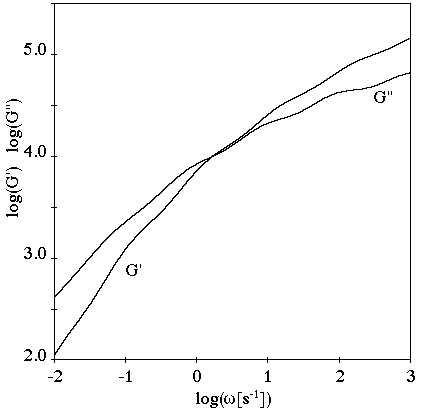
For oscillatory shear flow, the wiggles in Figure 6.60: Storage and Loss Moduli for Oscillatory Shear Flow are due
to the discrete relaxation spectrum. There is one wiggle for each relaxation
time, at .
A comparison of the Wagner and PSM damping functions for oscillatory shear flow is shown in Figure 6.61: Comparison of Damping Functions for Oscillatory Shear Flow.
The damping functions are equivalent for small values of invariant
. For large values of
, the Wagner damping function decreases more quickly than
the PSM function (
).
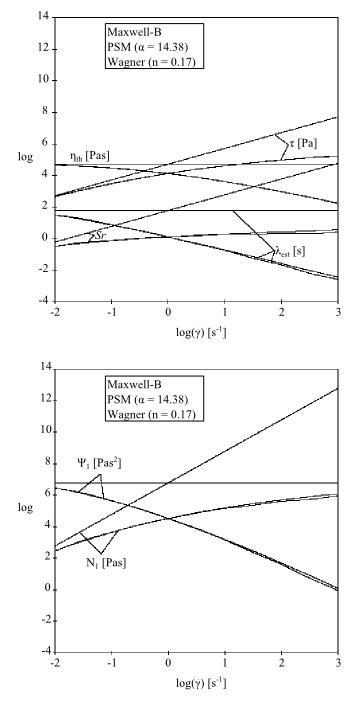
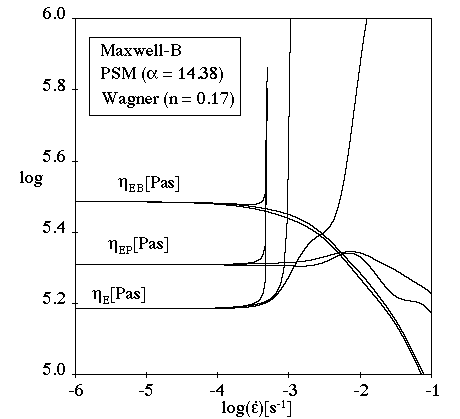
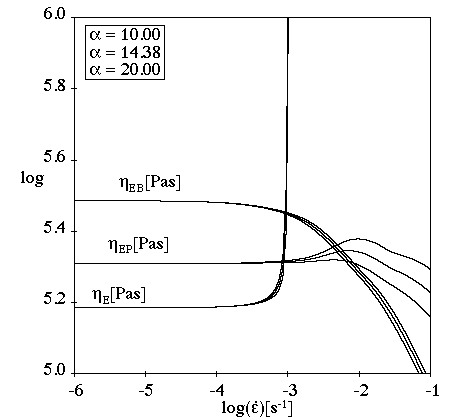
Figure 6.62: Comparison of Damping Functions for Simple Shear Flow
shows a comparison of the Wagner and PSM damping functions for a simple
shear flow. Shear thinning and a nonlinear are observed for both functions. The first normal-stress
difference is non-quadratic for both functions, with
. The first normal-stress coefficient is non-constant for
both functions, with
. The second normal-stress difference and the second
normal-stress coefficient are 0 for both.
is nonlinear and shows asymptotic behavior. For large
shear rates,
.
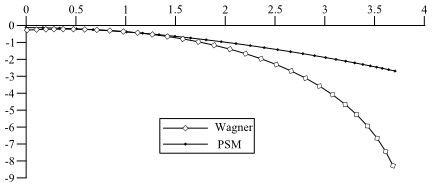
Figure 6.63: Comparison of Damping Functions for Extensional Flow
(β=0) shows a
comparison of the Wagner and PSM damping functions for an extensional flow,
with =0.
For the Wagner function, ,
, and
are bounded. For the PSM function,
is unbounded and
and
are bounded. For small extension rates, the type of
damping function has no effect on the extensional viscosity. For large
extension rates, the type of damping function strongly affects the
extensional viscosity.
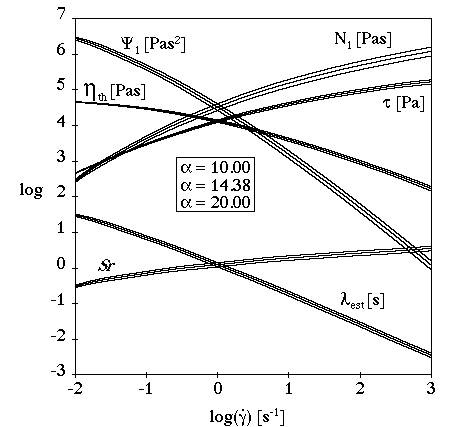
Figure 6.64: Effect of α (or n) on the PSM Damping Function for Extensional
Flow (β=0)
shows the influence of (or
) for an extensional flow with the PSM damping function and
=0.
(or
) has little effect on the viscometric curves or the
extensional viscosities. For
(or
=0), the behavior becomes the same as for Maxwell models.
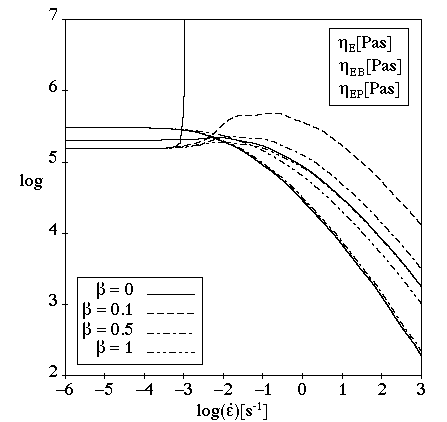
Figure 6.65: Effect of β on the PSM Damping Function for Steady Extensional
Flow (α=14.38) shows the influence of for an extensional flow with the PSM damping function and
=14.38.
is very sensitive to
,
is affected around
=1, and
is not affected by
. Note that
has no influence on shear viscosity.
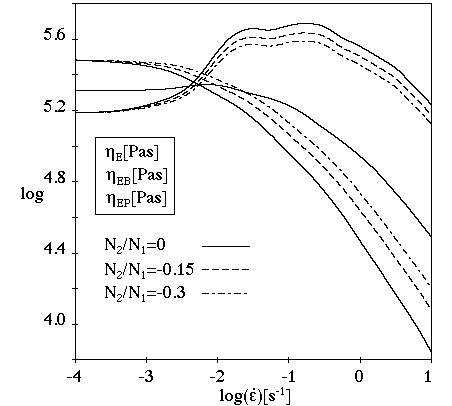
Figure 6.66: Effect of θ on the PSM Damping Function for Steady Extensional
Flow (α=14.38, β=0.1) shows the influence of for an extensional flow with the PSM damping function and
=14.38,
=0.1.
When decreases,
decreases,
increases, and
is not affected. Note that, in a simple shear flow, the
viscometric functions (except the second normal-stress difference and
coefficient) are independent of
.
Figure 6.67: Comparison of Damping Functions for Transient Shear Flow
(β=0)
shows a comparison of the Wagner and PSM damping functions for a transient
shear flow, with =0.
For the Wagner function, the overshoot is more significant, especially for the first normal-stress coefficient. The final value of the first normal-stress coefficient is lower for the Wagner function than for the PSM function. While the transient behavior depends upon shear rate, it is independent of the reversibility of the damping function.
Figure 6.68: Effect of α (or n) on the PSM Damping Function for Transient
Shear Flow (β=0)
shows the influence of (or
) for a transient shear flow with the PSM damping function
and
=0.
(or
) has little effect on the development of the transient
viscosity and the first normal-stress coefficient. It affects only the final
value of the viscosity and the first normal stress.
In the reversible PSM damping function, can increase or decrease, and in the irreversible
function,
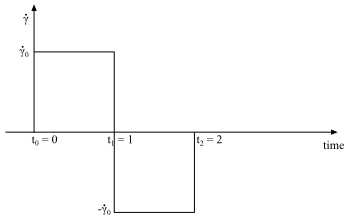
can only decrease. To illustrate the difference between
reversible and irreversible damping functions, consider a shear-rate history
that is a function of time. As shown in Figure 6.69: Transient Shear Rate Function, the
shear rate is equal to
for
, whereas it becomes
for
.
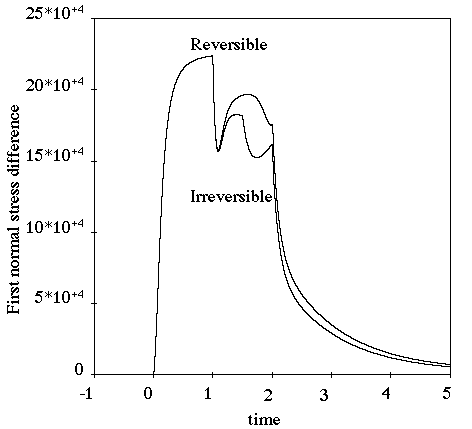
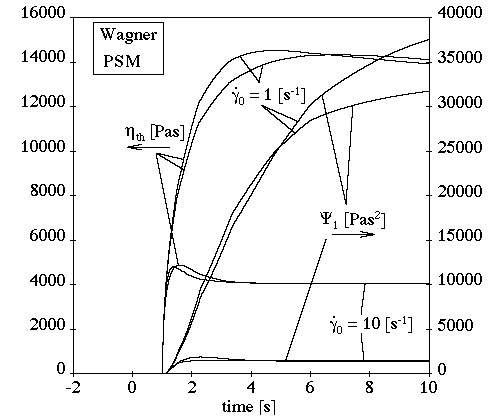
Figure 6.70: Comparison of Reversible and Irreversible PSM Damping Functions for
Transient Shear Flow (α=14.38)
shows a comparison between the reversible and irreversible PSM damping
function for a transient shear flow with =14.38. The first normal-stress difference for the
irreversible function is less than or equal to the first normal-stress
difference for the reversible function. As a result, the swelling with the
irreversible function is less than with the reversible function.
Figure 6.70: Comparison of Reversible and Irreversible PSM Damping Functions for Transient Shear Flow (α=14.38)