Kinematic conditions dictate boundary displacements in the normal direction only. In an Eulerian formulation, displacements of the interior nodes are not prescribed, and you can freely select internal node positions so as to minimize mesh deformation. It is also perfectly valid to move nodes tangentially along boundaries, since such displacements do not interfere with the kinematic conditions. Most remeshing techniques will also guarantee a tangential smoothness of the mesh along boundaries.
In Ansys Polyflow, remeshing techniques are based only on the positions and displacements of the boundary nodes, and not on kinematic considerations, unless a Lagrangian or streamwise method is used for remeshing. In many cases, it is impossible to maintain good mesh regularity without relocating nodes tangentially to the domain boundary. Tangential remeshing preserves the original node distribution along a line for 2D moving domains, and along a surface for 3D moving domains.
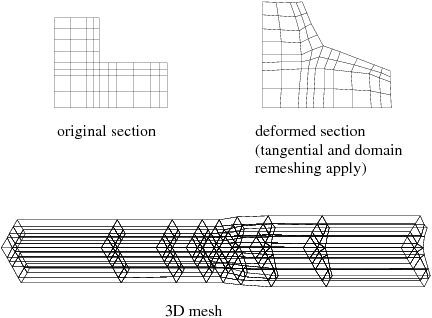
Figure 16.1: Tangential and Domain Remeshing shows tangential and domain remeshing. Note the following:
The kinematic condition controls the displacements along directors
, except with the line kinematic condition, where any displacement can occur in a plane orthogonal to the direction of extrusion.
Each kinematic condition introduces a tangential displacement along adjacent free surfaces or boundary sets.
Remeshing in the interior of the domain is based on the nodal displacements on the boundary.
In Figure 16.1: Tangential and Domain Remeshing, the normal displacement of nodes on the free surfaces is controlled by the kinematic equation; a tangential remeshing is applied on the planes of symmetry, while the position of the internal nodes is controlled by a remeshing technique.
In Ansys Polyflow, these operations occur simultaneously. Constraints resulting from kinematic conditions generate tangential remeshing constraints. All boundary displacements (whether tangential or normal) are substituted into the internal domain remeshing rule, so that a full system of constraints between all nodal displacements is assembled. A full Newton-Raphson scheme on all nodal positions (interior and on the domain boundary) is derived.