Most steady-state viscoelastic flow problems require an evolution scheme to
converge. For integral viscoelastic flow, the evolution scheme consists of
increasing from 0 to 1 by small steps until convergence is obtained at
(see Numerical Method for Integral Viscoelastic Flow
for details). In other words, the viscoelastic stress is increased while its
Newtonian counterpart decreases. Typical evolution parameters are given in Table 11.1: Evolution Parameters for Integral Viscoelastic Calculations.
Table 11.1: Evolution Parameters for Integral Viscoelastic Calculations
| Parameter | Value |
|---|---|
|
| 0 |
|
| 1 |
|
| 0.01 |
|
| 0.05 |
|
| 0.0001 |
| prediction | explicit Euler |
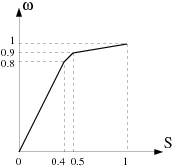
At the beginning of the evolution (),
increases quickly because the solution is easy to obtain. Near the
end of the evolution (
)
increases very slowly. The law that Ansys Polyflow uses to link
to
(shown in Figure 11.1: ω as a Function of S) reflects this behavior.
Here, continuity in the evolution scheme is achieved at ; that is, the solution of the initial flow problem is identical to
the limit of the evolution scheme for
. Toward the end of the evolution task (usually around
), convergence can become very slow. In order to avoid unnecessary
iterations, you may want to start the post-convergence task directly from a
converged solution at
. See also Additional Strategies for Convergence.