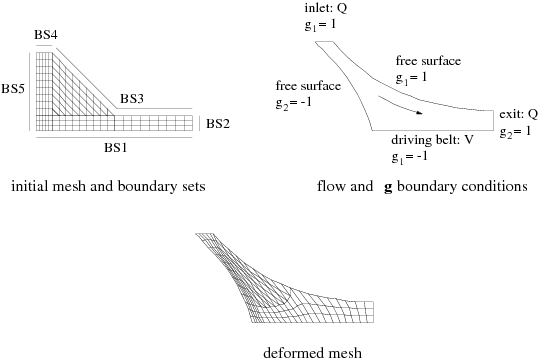
Consider the example shown in Figure 16.4: Coating Example for Thompson Transformation. This flow problem models a coating process, which involves two free surfaces. A Thompson transformation is used for the whole domain, since large mesh deformations are expected. The boundary conditions are described as follows: the fluid enters the flow domain at the top, is driven at the bottom by a belt that moves from left to right, and exits the computational domain on the right-hand side; the two remaining sides are free surfaces.
Five boundary sets are defined in Figure 16.4: Coating Example for Thompson Transformation,
and boundary conditions are selected so that the mesh domain maps logically onto a
square (2D) or cube (3D) region. The choice of or
is not always unique. Values on opposite sides of the square or
cube must be different, but the value itself is not relevant. For this reason,
values of 1 and
are generally used. On BS1, a value of
for
is imposed. On BS3 and BS4,
; on BS2,
; and on BS5,
. In general, a zero-normal-derivative condition is imposed on
boundary sets without an imposed component, in order to close the problem. A
zero-normal-derivative condition is therefore imposed for
on BS2 and BS5, and for
on BS1, BS3, and BS4. Ansys Polyflow will calculate the solution of
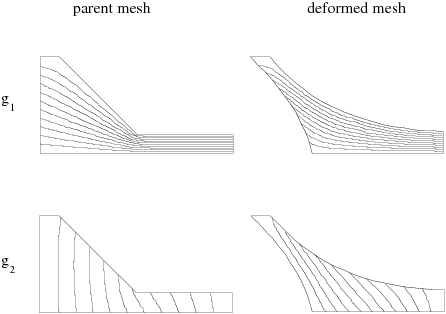
the Laplace equation for both
and
. This solution is shown in Figure 16.5: The g Field for the Thompson Transformation.
Then, upon deformation of the mesh, Ansys Polyflow will relocate nodes in such a way
that
and
are unchanged for a given node. Contour lines of the
and
fields are shown on the deformed and original (parent) meshes in
Figure 16.5: The g Field for the Thompson Transformation. The corresponding mesh is shown in Figure 16.4: Coating Example for Thompson Transformation.