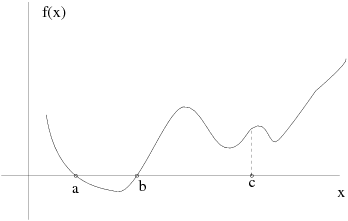
For several reasons, nonlinearity often makes computations difficult. Nonlinear problems frequently have multiple families of solutions. Also, the solution for a given set of parameters cannot generally be extrapolated from an initial, linear solution, since dramatic changes in the nature of the flow can occur with a slight change of flow parameters.

Typically, the solution of a nonlinear problem is surrounded by a domain of convergence. You can expect to reach the solution only if your initial guess lies within this domain. An example of this is the following. Suppose you want to find a solution to where is the function graphed in Figure 28.1: A Nonlinear Problem: . There are two solutions, and , but it will be difficult to find when starting from .

Figure 28.1: A Nonlinear Problem:

In most cases, the only way to solve a nonlinear problem is to begin with a solution to a simpler problem, one in which nonlinearity is not as troublesome. From this solution, you then solve a sequence of problems of increasing nonlinearity, using the solution of one problem as the initial condition for the subsequent problem. Ultimately, the sequence should lead to the original problem and its solution.

Suppose that, in the original problem, a certain parameter (such as density) that has value is found (or is suspected) to be largely responsible for the nonlinear nature of the problem. You can then consider a sequence of problems, in each of which this parameter is given the value , where . The sequence begins with ; if a solution is obtained with the parameter having value , then is increased, by a small amount, to , and a new problem is created with parameter value . If a solution is obtained, then the procedure is continued, using a larger value of the increment, such as . If the problem diverges, then the previous solution is returned to and a smaller increment, such as , is tried.

At each step, there is a limit to how much can be increased. Each problem solution can be used successfully as the initial condition for only those problems with sufficient proximity to the initial condition. Increasing by too much will result in a problem setup that will diverge with the previous solution used as an initial condition.

The evolution procedure in Ansys Polyflow is more general than that described above. Instead of assigning the parameter the value , you can choose a function and use the value for the parameter. You can also have increase over any interval, instead of requiring . Though evolution can be applied to more than one parameter, it is generally most effective when applied to a single parameter (with some exceptions, such as when applied to flow rate and pulling velocity).