
This node allows you to open a optiSLang monitoring database file (*.omdb) and modify data and filter settings.
There are settings that define the method to deal with the given data in order to train and test the possible approximation models and there are settings that define the method to find the optimal subspace for every output parameter. You can deselect all filters, then the algorithm will search for the optimal metamodel using the full parameter model.
Note: The current optiSLang version does not support nominal discrete parameters in MOP calculations.
You can export a MOP as a Functional Mock-Up Unit for use in a variety of simulation environments.
Further information about methods of metamodelling used in optiSLang can be found here.
To access the following tabs and options, double-click MOP on the Scenery pane.
Basic Settings
The MOP dialog provides a decision tree which helps to find a suitable model with good and proofed settings. Some information about the metamodels to test and filtering of variables is required.
| Option | Description |
|---|---|
| Tested metamodels | Select a group of metamodels to consider. |
| Variable reduction | Select a rule for filtering to reach the reduction of parameter space. |
| Write cross validation values | Add cross validated values to postprocessing file. |
Advanced Settings
If you select the check box, a property tree is displayed with all of the available settings.
| Option | Description | ||
|---|---|---|---|
| Testing type | Select the method of the test point determination. | ||
| Approximation type | Select either smoothing models (Polynomials, MLS with exponential weights or Kriging) or use interpolating models (MLS with regularized weights). | ||
| Resampling for single CoPs | The single Coefficient of Prognosis (CoPs) are estimated by varianced based sensitivity analysis on the final metamodel. If you select , the marginal distributions are generated by using the empirical distribution functions. Otherwise uniform distributions within the lower and upper bounds are assumed. | ||
| Max. responses in parallel | Sets the maximum number of responses to be calculated in parallel. | ||
| Use incomplete designs | When selected, designs with missed but at least one calculated responses are also used for creating the metamodel. | ||
| Export FMU after MOP creation | When selected, exports the MOP as a Functional Mock-Up Unit. | ||
| Adapt bounds | Adapts the boundaries of the resulting parameters to the sampling. An additional percentage factor of safety for the adapted boundaries can be added. The new boundaries are calculated by: 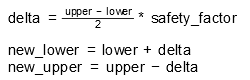 | ||
| CoP tolerance | Specifies the range for the CoP values in which a simpler model should be selected. The variable tolerance is used to automatically remove all variables below this tolerance from the best model. If is selected, the number of model coefficients is considered to penalize the CoP in order to prefer simpler models with similar prognosis quality. | ||
| Transformation | Enables or disables Box Cox transformations. | ||
| Models | |||
|
Select which metamodel types are tested. At least one model type has to be selected. Polynomial regression with linear and quadratic basis functions (order 1 and 2) and Moving Least Squares with linear and quadratic basis functions are available as well as ordinary Kriging with isotropic and anisotropic kernel functions. By means of the coefficient factor, the minimum number of samples for a specific model is defined. If the number of model coefficients times the coefficient factor exceeds the available number of samples, than this model candidate is not considered. An extra feature is using external models. Currently ASCMO is available on Windows platforms. This model can only be selected if Testing type is set to . Custom Script Surrogates are supported. | |||
| Filter | |||
| Significance Filter | Select the minimal quantile for the significance filters. This means that all possible significance filter configurations, defined by quantiles which are varied from 99% down to this minimal value, will be tested. | ||
| Importance Filter | Define an upper bound for the COI limits. The threshold minimal COI value is varied from 1% up to this bound and that defines another filter criterion for the input parameters. | ||
| Correlation Filter | Choose the number of steps in which the correlation coefficients of the remaining input parameters (after the significance filter) are divided. Each of the correlation coefficients determined that way defines a lower bound for a correlation filter. | ||
| CoD Filter | Define an upper bound for the CoD limit. The threshold minimal CoD value is varied from 1% up to this bound and that defines another filter criterion for the input parameters. | ||
| Input Correlations Filter | The input correlation filter removes strongly correlated input variables from the parameter subspace before the other filters are applied. Only if the Check value is exceeded by at least one input correlation, this filter is executed. Only correlations larger as the Minimum value are considered. The filter removes all variables having a multi-dimensional correlation larger than the Maximum value. | ||
| Algorithm messages | Show algorithm messages in project log or write to a separate file including the function strings for polynomials. | ||
| Crossvalidation values | Define the usage and naming of crossvalidated values. | ||
Show Postprocessing
When selected, opens postprocessing.
Inputs
For parameters, you can specify the importance manually when either the Variable reduction setting is set to or the check box is selected. Possible values are:
Outputs
For responses, you can specify whether or not to generate a metamodel. Select or clear the check box.
Additional Options
To access the options shown in the following table, in any tab, click .
| Option | Description |
|---|---|
| Auto-save behavior |
Select one of the following options:
The project, including the database, is auto-saved (depending on defined interval) after calculating this node/system (either when the calculation succeeds or fails). By default, is selected. |
| Retry execution | When selected, retries a node execution if it failed. Set the
following options:
|
Slots
| Slot Name | Slot type | Data type | Description | ||||
|---|---|---|---|---|---|---|---|
| In | Out | ||||||
| MDBPath | X |  | MOP result file of type *_MOP.bin, *.omdb, *.ascmo. | ||||
| Designs | X |  | Used support points of MOP. | ||||
| ParameterManager | X |  | All parameters that are used for MOP with corresponding properties. | ||||
| ShowPPWhenAvailable | X |  | Show Postprocessing? yes/no | ||||
| MDBPath | X |  | The MOP results file which can be used for MOPsolver. | ||||
| CoDadj | X |  | The adjusted coefficient of determination of all responses. | ||||
| COP | X |  | The coefficient of prognosis of all responses (predictive coefficient of determination for Leave one out). | ||||
| FoundModel4Response | X |  | The information for each response if a model was found. | ||||
| ParameterManager | X |  | Filtered parameters found by MOP. | ||||
| SingleCOP | X |  | The coefficient of prognosis for single inputs (predictive coefficient of determination for Leave one out). | ||||
Available Models for Scalar Outputs
For scalar outputs, the following models are available within the MOP competition:
Polynomial regression with linear and quadratic basis functions (order 1 and 2)
Moving Least Squares (MLS) with linear and quadratic basis functions
Ordinary Kriging with isotropic and anisotropic kernel functions
Genetic Aggregation Response Surface (GARS)
Support Vector Regression (SVR)
Deep Feed Forward Network (DFFN) – requires Enterprise license
Deep Infinite Mixture Gaussian Process (DIM-GP) – requires Enterprise license
The polynomial model is the simplest but the fastest available model. It can be applied for small, medium, and even large number of samples. The approximation of the model with the MOP solver and within the exported Functional Mock-Up Unit (FMU) is also faster than all other available models. Moving Least Squares and Kriging are more time consuming for the model training, especially the anisotropic Kriging, which limits an efficient application up to 1000 samples. You can export these modules as FMU and are fast in the approximation. MOP filtering is applied to reduced the active variables to the important ones.
Genetic Aggregation Response Surface (GARS) and Support Vector Regression (SVR) are metamodels from DesignXplorer. GARS is similar to the anisotropic Kriging limited to smaller data sets due to exponential increasing training time. Support Vector Regression (SVR) can be applied even for larger data sets. Both models use the MOP filtering for variable selection. You currently cannot export FMU for these models.
The Deep Feed Forward Network (DFFN) is a deep learning neural network with automatic feature and variable filtering (smart layout). The training of this model becomes efficient for large data sets with more than 1000 samples, where the training of other models such as MLS, Kriging, or GARS becomes inefficient.
Deep Infinite Mixture Gaussian Process (DIM-GP) is a further development of the Kriging approach, using a more flexible covariance matrix description represented by a neural network approximation. The DIM-GP model can be efficiently trained up to 2000 samples. Currently, variable filtering is not available within the MOP node for the DIM-GP model. Similar to GARS and SVR,you cannot export the DIM-GP and the DFFN models as FMU.
The following table describes the properties and a suggested application for each model.
| Model | Number of Training Samples | Variable Filtering | MOP Solver Performance | FMU Export | Recommendation |
|---|---|---|---|---|---|
| Polynomial | All | MOP filter | Very fast | Yes |
Fast training and fast evaluation, should always be tested. |
| MLS | ≤ 2000 | MOP filter | Fast | Yes |
Good quality with fast training and fast evaluation (for example, digital twin). |
| Isotropic Kriging | ≤ 2000 | MOP filter | Fast | Yes |
Good quality with fast training and fast evaluation (for example, digital twin). |
| Anisotropic Kriging | ≤ 500 | MOP filter | Fast | Yes |
Focus on best quality fast evaluation (for example, digital twin). |
| GARS | ≤ 500 | MOP filter | Medium | No | Focus on best quality. |
| SVR | ≤ 5000 | MOP filter | Medium | No | Focus on best quality. |
| DFFN | ≥ 500 | Smart layout | Medium | No | Works best for large data sets. |
| DIM-GP | ≤ 2000 | No | Slow | No | Focus on best quality. |
Looking at possible use cases, you can distinguish between the following
Getting a good compromise between model quality and training time/model complexity.
Generate a surrogate model for a later use within a digital twin, for example, as an FMU export.
The competition should detect the best possible model with the best approximation quality from the available models, where the training time may be much larger as in the first use case.
The following table describes which models should be used for each use case, and provides suggestions for the number of training samples.
| Use Case | Number of Training Samples | Polynomial | MLS | Iso Kriging | Aniso Kriging | SVR | GARS | DFFN | DIM-GP |
|---|---|---|---|---|---|---|---|---|---|
| Good compromise between training time and model quality | N ≤ 200 | x | x | x | x | x | x | ||
| 200 < N ≤ 1000 | x | x | x | x | x | x | |||
| N > 1000 | x | x | x | ||||||
| Best quality model for FMU export/digital twin | N ≤ 500 | x | x | x | x | ||||
| 500 < N ≤ 2000 | x | x | x | ||||||
| N > 2000 | x | ||||||||
| Best quality model | ≤ 500 | x | x | x | x | x | x | x | x |
| 500 < N ≤ 2000 | x | x | x | x | x | x | |||
| N > 2000 | x | x | x |


