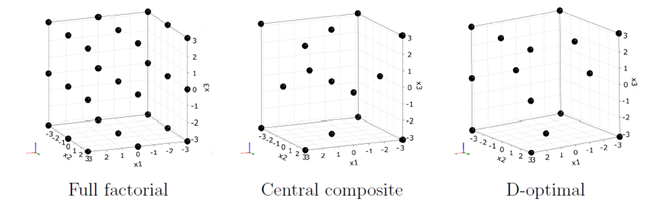
In order to perform a global sensitivity analysis, the space of the design variables has to be scanned by discrete realizations. Each realization is one set of values belonging to the specified inputs. As design exploration often deterministic Designs of Experiments (DoE) are applied (Myers and Montgomery 2002). These design schemes are mainly based on a regular arrangement of the samples, as in the full factorial design. Generally the number of samples increases exponentially with increasing dimension. Fractional factorial designs use only a part of the full factorial samples, however the number of levels in each direction is limited. In Figure 2.2: Classical Design of Experiment Schemes a few typical DoE schemes are shown.
The central composite design contains, additionally to the 2k full factorial design points, the midpoints of each hypercube surface. D-optimal designs are generated in order to represent a linear or quadratic function with optimal accuracy. Further details about classical DoE schemes, which are also available in optiSLang, can be found in (Myers and Montgomery 2002).
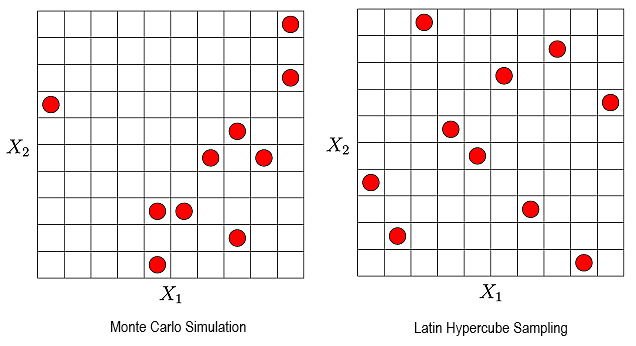
As alternatives to deterministic design exploration methods, stochastic sampling schemes can be applied. A very common approach is random sampling, which is called Monte Carlo Simulation (MCS). For design exploration the design variables are assumed to follow a uniform distribution with given lower and upper bounds. The random samples are generated independent in the given design space. If only a small number of samples is used, often clusters and holes can be observed in the MCS sampling set as shown in Figure 2.3: Stochastic Sampling Schemes.
More critical is the appearance of undesired correlations between the input variables. These correlations may have a significant influence on the estimated sensitivity measures. In order to overcome such problems, optiSLang provides optimized Latin Hypercube Sampling (LHS) (McKay, Beckman, and Conover 1979), where the input distributions and the specified input correlations are represented very accurately even for a small number of samples. In the standard Latin Hypercube approach the minimization of the undesired correlation is performed by using the method according to (Iman and Conover 1982). Furthermore an advanced Latin Hypecube Sampling (ALHS) is available, where the correlation errors are minimized by stochastic evolution strategies (Hungtington and Lyrintzis 1998). This approach is recommended if the number of input variables is less than 50.
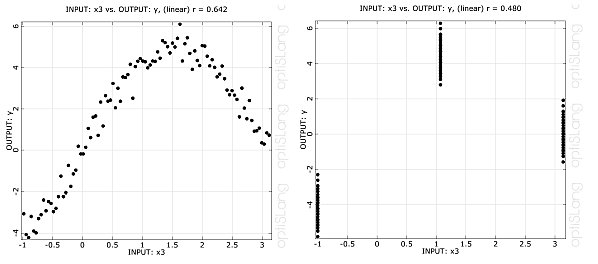
Compared to Latin Hypercube sampling deterministic design schemes have two main disadvantages: They are limited to a small number of variables due to the rapidly increasing number of required samples when increasing the model dimension. Further, a reduction of the number of inputs does not improve the information gained from the samples, since only two or three levels are used in each dimension. This is illustrated in Figure 2.4: Dimension Reduction. In this figure, a nonlinear function having one major and four almost unimportant variables is evaluated. Using the LHS, the nonlinearity can be represented very well in the reduced space. In the case of the full factorial design, which contains three levels in each directions, again only three positions are left in the reduced space and the dimension reduction does not allow a better representation of the model response.