VM-LSDYNA-SOLVE-016
VM-LSDYNA-SOLVE-016
Thermal Expansion of a Cylindrical Bar with Temperature Dependent Thermal Expansion
Coefficient
Overview
| Reference: | Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co. |
| Analysis Type(s): | Thermal Expansion |
| Element Type(s): | Solid |
| Input Files: | Link to Input Files Download Page |
Test Case
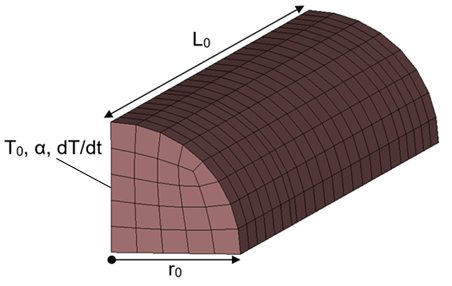
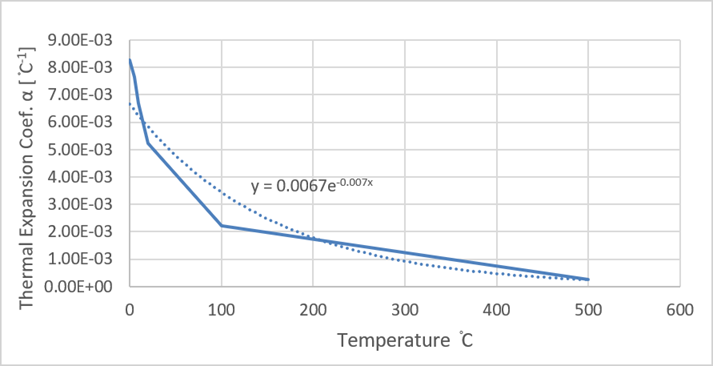
A cylindrical Uranium bar with length L0 = 0.110625 m and radius r0 = 0.0125 m has initial temperature T0 = 0° C. The bar has constant thermal generation rate of 5000°C/s. The linear thermal expansion coefficient as a function of temperature is defined below:
| Temperature °C | Thermal Expansion coef. α [°C-1] |
| 0 | 2.752E-03 |
| 5 | 2.548E-03 |
| 10 | 2.227E-03 |
| 20 | 1.745E-03 |
| 100 | 7.44E-04 |
| 500 | 9.03E-05 |
Find the ratio of bar volume at t = 0.1 s to initial volume (Vf/V0).
| Material Properties | Geometric Properties | Loading |
|---|---|---|
| k = 1 W/(m° C) | L0 = 0.110625 m | α = (see table) |
| h = 1 W/(m2 °C) | r0 = 0.0125 m | dT/dt = 5000° C/s |
| – | – | T0 = 0° C |
Analysis Assumptions and Modeling Notes
LS-DYNA Thermal Solver 11 is used. FWORK in *CONTOL_THERMAL_SOLVER is set to 1E–20 to turn off plastic deformation heating. The bar is made of solid elements with ELFORM 1. Constant thermal generation in the bar is defined in *MAT_THERMAL_ISOTROPIC. The coefficient of thermal expansion and other temperature dependent material properties are defined in *MAT_ELASTIC_PLASTIC_THERMAL.
An alternate method to *MAT_ELASTIC_PLASTIC_THERMAL is to reference a curve defining the thermal expansion coefficient as a function of temperature in *MAT_ADD_THERMAL_EXPANSION. Other material properties would be defined in *MAT_ISOTROPIC_ELASTIC_PLASTIC.
Symmetry is exploited so only a quarter of the bar is present.
The volumetric thermal expansion coefficient, β, as a function of temperature can be approximated by the equation:
The volumetric thermal expansion coefficient can be written as:
Combining equations gives the following:
Integrating LHS from V0 to Vf and RHS from T0 = 0°C to Tf = 500°C gives us the analytical solution of (Vf/V0) = 2.53.
Results Comparison
The error shown in the Results Table may be due to the fitting method of the thermal expansion coefficient as a function of temperature. LS-DYNA uses the temperature and thermal expansion coefficient points mentioned in the Test Case Description, while the analytical solution uses a best-fit line of those points.
| Results | Target | LS-DYNA | Error (%) |
|---|---|---|---|
| Volume Ratio (Vf/Vo) | 2.530 | 2.547 | 0.7% |