VM-LSDYNA-SOLVE-013
M-LSDYNA-SOLVE-013
Transient Thermal Conduction of 3 and 4 Node Shell Elements
Overview
| Reference: | Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co. |
| Analysis Type(s): | Transient Thermal |
| Element Type(s): | Shell |
| Input Files: | Link to Input Files Download Page |
Test Case
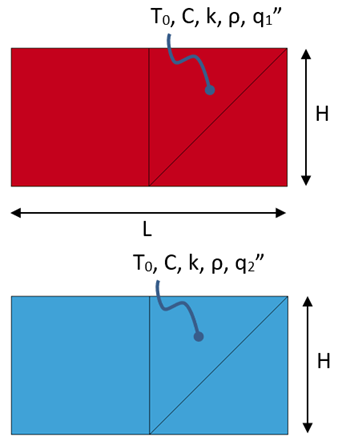
Two slabs have length 2 m, height 1 m, and thickness 1 m. The initial temperature, T0, of each is 1000°C. A constant flux of q1" = -1.0 W/m2 and q2” = 1.0 W/m2 is applied to each slab, respectively, on the top and bottom surfaces. The slabs have density ρ = 1kg/m3 and specific heat C = 1.0 J/kg °C. Find the temperature of each slab at t = 100 s
| Material Properties | Geometric Properties | Loading |
|---|---|---|
| k = 1 W/(m °C) | L = 2.0 m | T0 = 1000°C |
| C = 1.0 J/kg °C | d = 1.0 m | q1" = -1.0W/m2 |
| ρ = 1 kg/m3 | H = 1.0 m | q2" = 1.0W/m2 |
Analysis Assumptions and Modeling Notes
LS-DYNA Thermal Solver 1 is used. Shell elements with ELFORM 1 and thickness 1.0 m are used. The mesh of each slab is comprised of one four-node shell and two three-node shell elements. The initial temperature is set using *INITIAL_TEMPERATURE. The constant surface flux is defined using *BOUNDARY_FLUX. LOC is set to -1 and 1 to apply flux on both the top and bottom surface of shells. TSHELL is set to 1 in *CONTROL_SHELL to allow conduction through thickness of shells. Structural material properties are defined using *MAT_RIGID. Thermal material properties are defined in *MAT_THERMAL_ISOTROPIC.
Consider the rate of heat flow from both the top and bottom surfaces:
The same equation can be expressed as:
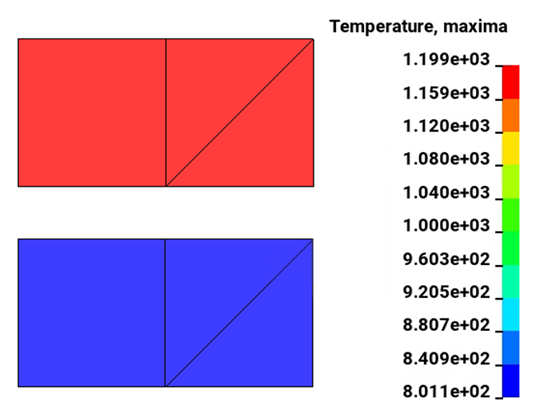
LHS is integrated from t = 0 to t = 100 s. And RHS is integrated from T0 = 1000°C to Tf,. When q1" = -1.0 W/m2 and q2" = 1.0 W/m2, the slabs have final temperature Tf = 1200°C and Tf = 800, respectively, at t = 100 s.