VM-LSDYNA-SOLVE-012
VM-LSDYNA-SOLVE-012
Steady State Thermal Analysis of 2D Axisymmetric Cylindrical Shell
Overview
| Reference: | Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co. |
| Analysis Type(s): | Steady State Thermal 2D Axisymmetric |
| Element Type(s): | Shell |
| Input Files: | Link to Input Files Download Page |
Test Case
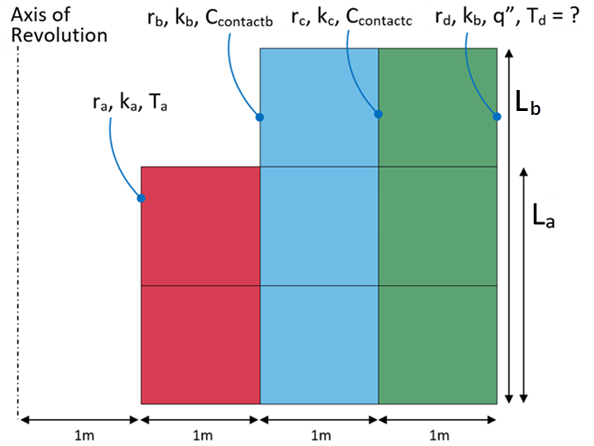
A cylindrical shell has inner radius temperature Ta = 0°C. The length of the cylinder is 2 m from ra = 1 m to rb = 2 m. The length of the cylinder from rb = 2m to rd = 4 m is 3 m. The outer surface has a flux of -20 W/m2. Find the steady state temperature of the outer surface Td. Heat transfer conductance at the contact surface rb = 2 m and rc = 3 m is set as 1000 W/°C
| Material Properties | Geometric Properties | Loading | Thermal Contact |
|---|---|---|---|
| ka = kb = 1 W/(m°C) | La = 2.0 m | q" = -20W/m2 | Ccontactb = 1000 W/°C |
| – | Lb = 3.0 m | Ta = 0°C | Ccontactc = 1000 W/°C |
| – | ra = 1.0 m | Td = ? | – |
| – | rb = 2.0 m | – | – |
| – | rd = 4.0 m | – | – |
Analysis Assumptions and Modeling Notes
LS-DYNA Thermal Solver 1 is used. Three separate parts of equal material make up the model. Section shell with ELFORM 15 and thickness 0.001 m is used to create the 2D axisymmetric elements. *BOUNDARY_TEMPERATURE is used to set the boundary temperature on ra. A flux boundary condition is set on the outer surface, rd, using *BOUNDARY_FLUX. Heat transfer conductance is specified between parts using *CONTACT_2D_AUTOMATIC_SURFACE_TO_SURFACE_THERMAL.
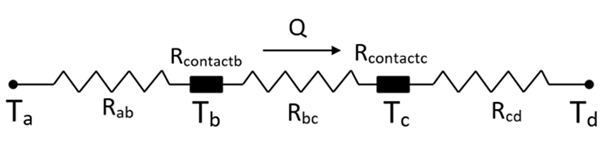
At steady state, the rate of heat dissipation Q is
where
And the conduction resistances Rab, Rbc, and Rcd, and for cylindrical shell can be expressed as below
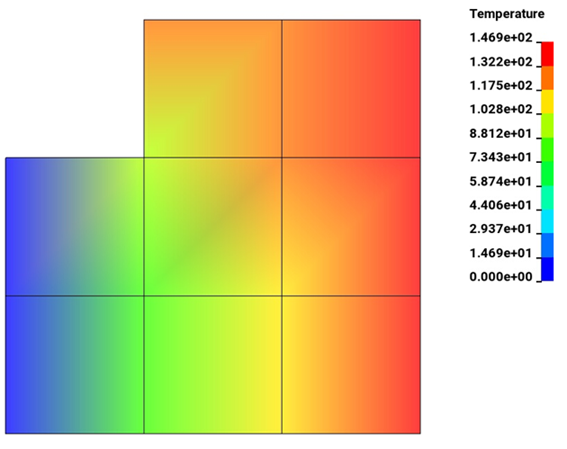
From the above equations, the analytical solution of Td is obtained as 141.644°C.