VM-LSDYNA-SOLVE-005
VM-LSDYNA-SOLVE-005
Steady State Thermal Analysis of 3D Spheres with Internal Heat
Generation
Overview
| Reference: | Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co. |
| Analysis Type(s): | Steady State Thermal |
| Element Type(s): | Solid |
| Input Files: | Link to Input Files Download Page |
Test Case
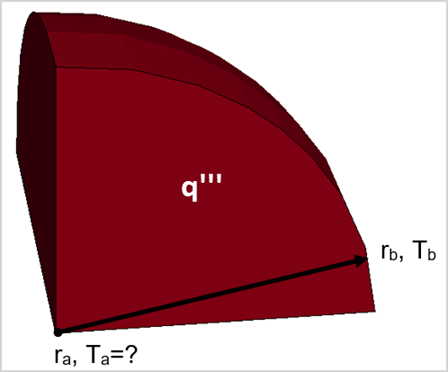
A sphere has an outer surface temperature Tb of 0°C at rb = 5.0 m. The material of the sphere is isotropic with specific heat c. The sphere has a constant heat generation rate per unit volume q''' = 1 W/m3. Compute the steady state temperature at the center of the sphere at ra = 0 m.
| Material Properties | Geometric Properties | Loading |
|---|---|---|
| k = 1 W/(m°C) | ra = 0 m | Tb = 0°C |
| c=1 J /(kg°C) | rb = 5.0 m | q''' = 1 W/m3 |
Analysis Assumptions and Modeling Notes
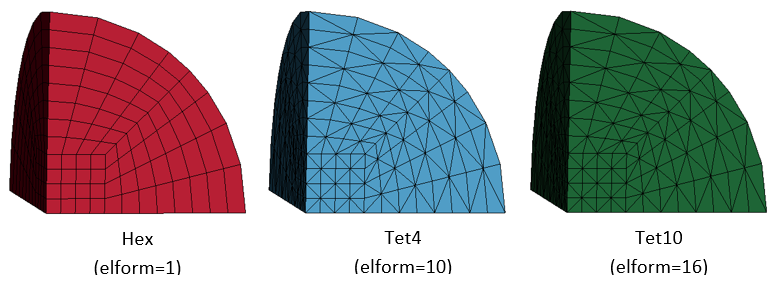
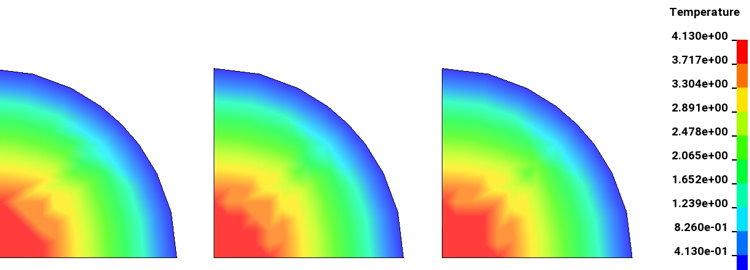
LS-DYNA Thermal Solver 11 is used. Three spheres in this example are modeled using ELFORM = 1, 4, and 16. The temperature boundary condition is applied using the keyword *BOUNDARY_TEMPERATURE. The constant heat generation rate is initiated by setting TGRLC to zero and TGMULT to one in *MAT_THERMAL_ISOTROPIC.
The modelling of the sphere is accomplished using one eighth symmetry. The heat flow is limited to be only in the radial direction.
The temperature inside a sphere with heat generation is expressed by:
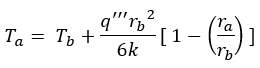
From the above equation, the analytical solution of Ta is obtained as 4.1667°C.