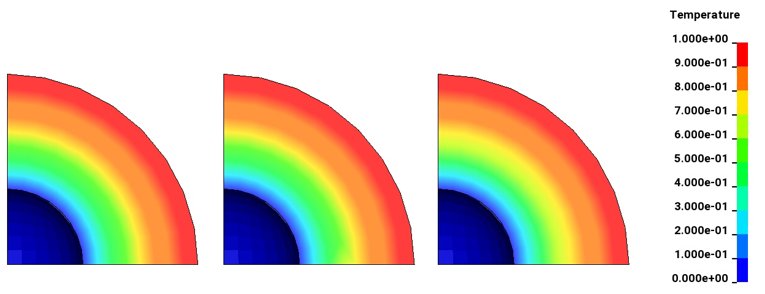VM-LSDYNA-SOLVE-004

VM-LSDYNA-SOLVE-004
Steady State Thermal Analysis of 3D Hollow Spheres with Temperature Boundary Condition

Overview

Reference:	Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co.
Analysis Type(s):	Steady State Thermal
Element Type(s):	Solid
Input Files:	Link to Input Files Download Page

Test Case

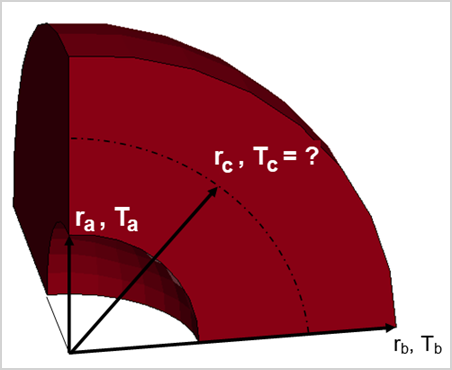
A hollow sphere has an inner surface temperature T_a of 0°C at r_a and an outer surface temperature of 1°C at r_b. The material of the hollow sphere is isotropic. Compute the steady state temperature at r_c = 3.51419 m.

Figure 23: Problem Sketch

Material Properties	Geometric Properties	Loading
k = 1 W/(m°C)	r_a = 2 m	T_a= 0°C
—	r_b = 5.02839 m	T_b = 1°C

Analysis Assumptions and Modeling Notes

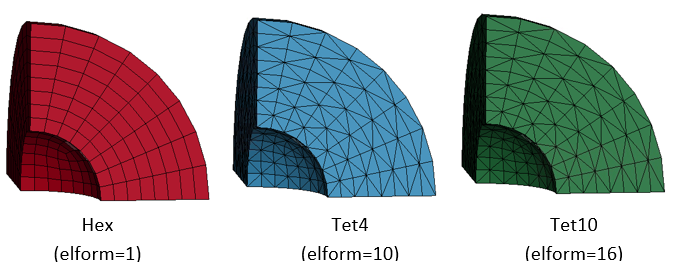
LS-DYNA Thermal Solver 11 is used. Three hollow spheres in this example are modeled using ELFORM = 1, 4, and 16. The temperature boundary conditions are applied using the keywords *BOUNDARY_TEMPERATURE.

The modeling of the sphere is accomplished using one eighth symmetry. The heat flow is limited to be only in the radial direction.

At steady state, the rate of heat dissipation Q:

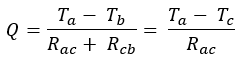
Where the thermal resistances R_ac and R_bc can be expressed as below:

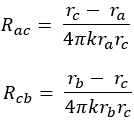
From the above equations, the analytical solution of T_c is obtained as 0.715438°C.

Figure 24: Hollow sphere models with hex, tet4 and tet10 element meshes

Figure 25: Fringe plot of temperature °C for each model

Results Comparison

	Target	LS-DYNA	Error (%)
Temperature at r_c (hex)	0.715438°C	0.714271°C	0.16%
Temperature at r_c (tet4)	0.715438°C	0.714746°C	0.097%
Temperature at r_c (tet10)	0.715438°C	0.721018°C	0.78%