- Growth Law
determines the height of the layers given the initial height and height ratio.
Linear
The prism height of a particular layer is calculated by
, where h = initial height, r = height ratio, and n = layer number.
The total height at layer n is
.
Exponential
The prism height of a particular layer is calculated by
, where h = initial height, r = height ratio, and n = layer number.
The total height at layer n is
.
WB-Exponential
This is the exponential growth law as defined in Ansys Workbench. The prism height of a particular layer is calculated by
, where h = initial height, r = height ratio, and n = layer number.
Figure 268: Prism Growth Law shows a box with edge length = 1, h = 0.05, r = 1.5, and n = 5, with different growth laws applied.
- Initial height
is the height of the first layer of elements.
Note: If the initial height is set to 0, it will be automatically determined by the local triangle size, where the height of the last layer will be the minimum attached triangle edge length times the Prism height limit factor.
- Height ratio
is the expansion ratio from the first layer of elements on the surface. This ratio will be multiplied by the element height of the previous layer to define the height of the next layer.
- Number of layers
is the number of layers to be grown from the surface or curve.
- Total height
is the total height of all the prism layers.
Note: If neither the initial height nor the total height is set, the prism layer heights will be "floating" in order to produce a smooth volume transition to the tetrahedra (see Figure 269: All Prism Heights Floating). In order to smooth the volume transition, the last prism layer height must not exceed a certain height-to-base ratio. This value is 0.5 by default, but can be adjusted using the Prism height limit factor.
The Prism height limit factor combined with the shortest edge of the base triangle for each column are used to calculate the last prism height for each column. This is combined with the growth ratio, number of layers and the growth law to back calculate the initial height required for each column in order to produce a smooth growth ratio. If you would rather have a fixed initial height, you can redistribute the prism layers later.
You can use a combination of floating prism layer height and prescribed initial/total height on selected entities/parts (see Figure 270: Combination of Prescribed and Floating Prism Heights). In this case, the initial height has been set on only the valve part. The prism heights on the valve part are now calculated using the specified initial height along with the growth law, ratio, and number of layers. All other prism heights remain floating.
- Compute params
will compute the missing parameter based on the given parameters if one of the parameter values is blank.
- Fix marching direction
if enabled, prisms are grown in a direction normal to the base triangles on the surface. However, the quality of mesh is still controlled by Min prism quality.
When Fix marching direction is enabled, directional smoothing applies only to the first layer. The initial direction is evaluated from the face normals attached to the vertex to be extruded. This is done by interpolation. For further layers, the direction is "fixed" and directional smoothing is disabled.
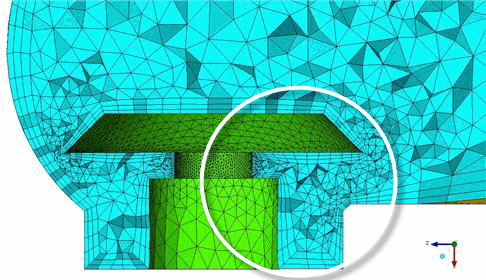
Figure 271: Use of the Fix Marching Direction Option
Fix Marching Direction Disabled
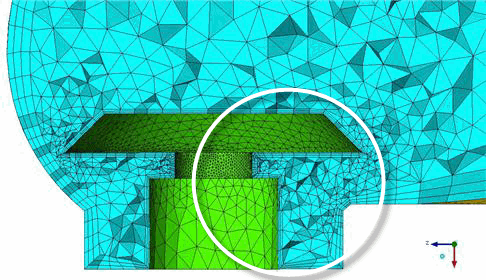
Fix Marching Direction Enabled
In the first example in Figure 271: Use of the Fix Marching Direction Option, Fix Marching Direction is disabled and the prism direction is controlled by the directional smoothing steps and the Ortho weight value. In the second example, Fix Marching Direction is enabled. The prisms grow normal to the surface, except in cases of extremely poor quality first layer elements.
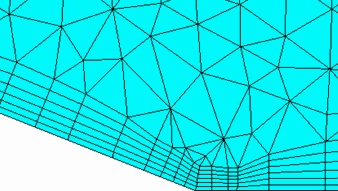
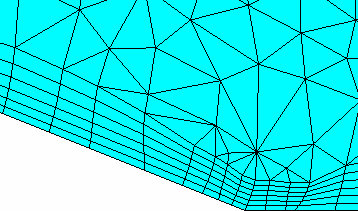
In the next set of examples in Figure 272: Fix Marching Direction Option, prisms were grown largely orthogonal to the base triangles up to the 3rd layer, beyond which the Min prism quality caused a change in direction. This method may be more appropriate when growing prism in the VORFN region.
Figure 272: Fix Marching Direction Option
Fix Marching Direction Enabled 
Fix Marching Direction Disabled 
Note: If you do not use any directional smoothing, the prism marching direction is already fixed.
- Min prism quality
locally prevents or adjusts prism growth in problem areas in order to maintain quality. Complex geometry combined with aggressive prism parameters may result in poor quality elements. If the quality does not meet the minimum value, the prism elements are re-smoothed directionally, or pyramids are used to replace some prism elements. Setting a value that is too high will result in local prism interruptions and more pyramids.
Table 7: Effect of Min Prism Quality and Initial Height demonstrates the effect of Min prism quality on prism mesh of two different initial heights.
Table 7: Effect of Min Prism Quality and Initial Height
Initial Height = 0.15, Growth Ratio = 1.2, Number of Layers = 5 Min prism quality value Actual Prism Quality 0.0 0.003 0.01 0.065 0.075 0.1 0.1 0.13 Initial Height = 0.1, Growth Ratio = 1.2, Number of Layers = 5 Min prism quality value Actual Prism Quality 0.0 0.146 0.01 0.146 0.075 0.146 0.1 0.146 In contrast, for the mesh with an Initial Height of 0.1, the prism quality is already higher than the Min prism quality value.
- Fillet ratio
tries to create a fillet proportional to the total height of the prism. When prisms are grown in the corner zone of a tet mesh, it is possible to control the prism layer smoothness along a fillet using this parameter.
Note: For meshing corners with angles less than 60 degrees, there may not be space for a fillet.
Figure 273: Examples of Fillet Ratio
Fillet Ratio = 0.0 means no fillets.
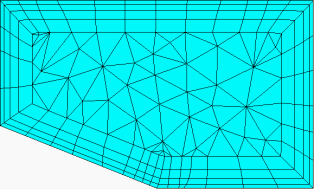
Fillet Ratio = 0.5 limits the radius of the inner prism fillet to 0.5 times the height of the total prism thickness.
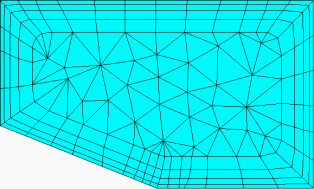
Fillet Ratio = 1.0 allows the radius of the inner prism fillet to equal the prism layer thickness.

Increasing the typically improves the internal angles of the prisms and results in more full prism layers in tight geometries. However, the increased prism height reduces the aspect ratio quality measure and may give bad angles in the triangle prism cap.
Note: For Fluent Meshing pre inflation prism growth, the parameter
offset-weightis equal tofillet ratio.- Max prism angle
controls prism layer growth around angles and when adhering to adjacent surfaces. This is the maximum internal angle between the base and the extruded direction. This parameter can range from 140 to 180 degrees. If extruding from one surface and not its neighbor, and the angle between the two surfaces is less than the specified value, the prisms will adhere to the adjacent wall.
For instance 135 is the theoretical minimum needed to go around a 90 degree corner (90+45 meeting up with the 90+45 coming from the other surface); to account for tolerances, the minimum setting is 140 degrees. A max prism angle of 180 allows the mesh to fold back on to its self, like at the trailing edge of a wing or a cusp between pipes in a manifold (90+90 meeting up with the 90+90 from the other side).
Figure 274: Max Prism Angle – Example 1
Max Prism Angle = 140 degrees Here, the angle between the planes is 158.2 (21.8) degrees. Since the Max prism angle is less than the angle between the walls, the prism layers are capped with pyramids.
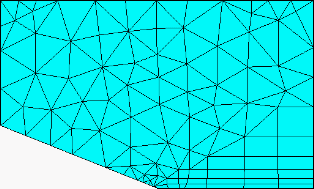
Max Prism Angle = 180 degrees Here, the Max prism angle exceeds the separation angle between the surfaces, so the prism remains attached to the adjacent surface.

Figure 275: Max Prism Angle – Example 2
Max Prism Angle = 140 degrees Here, the Max prism angle is set to 140, which is not enough to meet the prisms from the under side of the cusp.

Max Prism Angle = 180 degrees Here, the Max prism angle is set to 180 and the Min prism quality is set to 0.0001 so that the prisms from the top surface can meet the prisms from the lower surface. The prisms where the two surfaces meet have large internal angles and poor quality.

Note: Pyramids are usually not favorable. However in "cusp" situations such that exist on the trailing edge of a wing or within a manifold where two pipes meet at a slight angle, it is better to have the prism layer terminate with pyramids than try to wrap around the cusp. It is recommended that Max prism angle be set to 160 degrees, particularly for applications with cusp geometry.
Note: For Fluent Meshing pre inflation prism growth, the parameter
project-adjacent-angleis derived from this parameter using:project-adjacent-angle=max prism angle– 90 deg.- Max height over base
When the prism aspect ratio (ratio of height over base of the base triangle) reaches this value, the prism stops growing.
The examples in Figure 276: Max Height Over Base illustrate the use of this option for a 6 layer prism mesh.
Figure 276: Max Height Over Base
No Value Set for Max Height Over Base
In this case, the prisms with a smaller base have the same height as the prisms with wider bases. The resulting tall prisms have much greater volume than their adjacent tetra elements and are not considered ideal.
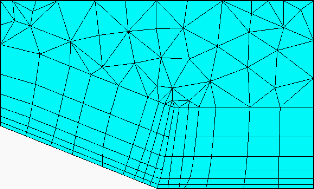
Max Height Over Base = 1.0
If the Max height over base is set to 1.0, then the prism height can not exceed the average base length. Prisms that would have exceeded this are not grown. Other prisms may not grow due to related quality issues.
Note: For the Fluent Meshing pre inflation method, this is the default value.

Max Height Over Base = 0.5
In this case, even the initial height would exceed this ratio for the elements in the corner, so no prisms are grown there. Generally, the initial height at the wall would be less than half the smallest element size.
Note: For Fluent Meshing pre inflation prism growth, the parameter
min-aspect-ratiois derived from this parameter using:min-aspect-ratio= 1.0 /max height over base.- Prism height limit factor
restricts the prism aspect ratio (height of each prism element over base size for each column) to the specified value by limiting the prism growth ratio, but maintains the number of layers.
If the initial height is set globally or on a part or entity, and the growing prism layers reach the specified aspect ratio, the growth ratio is reduced so that the height for additional layers will remain constant at that height limit factor (aspect ratio).
If the initial height is not set globally and not set on the part or entity, it will "float" (see the Total height section) to improve the transition to the tetrahedra. You can then use the prism height limit factor to control the transition by adjusting the maximum height-over-base ratio of the prisms. This will be used to calculate the initial heights on a column by column basis and so that a single growth ratio will be used and produce a smoother transition to the maximum prism height for each column. If the initial height is left to "float" and the prism height limit is not set, a value of 0.5 will be used to obtain smooth volume transition from the prisms to the attached tetra.
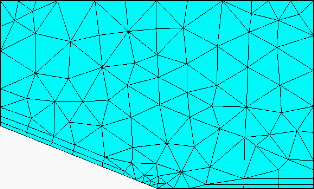
Figure 277: Prism Height Limit Factor
No Value Set for Prism Height Limit Factor 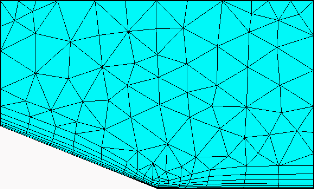
Prism Height Limit Factor = 0.5 
Prism Height Limit Factor = 1.0 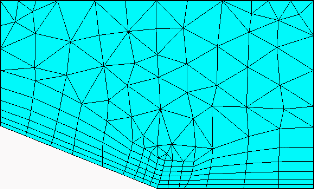
- Ratio multiplier
This is a global parameter that multiplies the Height Ratio for each successive layer when using the Exponential Growth Law, creating hyper-exponential growth. For example, if the Height Ratio is set to 1.2, and the Ratio multiplier set to 1.1, then the ratio between the first two layers will be 1.2, the ratio between the second and third layer will be (1.2 * 1.1), the ratio between the third and fourth layer will be (1.2 * 1.1 * 1.1), etc. The default value is 1.
The prism height of a particular layer is calculated by
, where h = initial height, r = height ratio, n = layer number, and m r = ratio multiplier.
The ratio at any layer is calculated using
, and will be limited by the Ratio max option under Advanced Prism Meshing.