When a liquid particle impinges a wall, the particle may deform and remain in direct contact with the wall for a short period of time before rebounding. During this time, heat is exchanged between the particle and the wall.

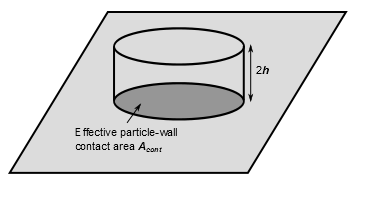
For droplet-to-wall heat transfer calculations, the Ansys Fluent discrete phase model assumes that the droplet deforms to a cylinder when impacting the wall (see Figure 12.16: Geometric Parameters of Deformed Impinging Droplet in Heat Transfer Calculations).

Figure 12.16: Geometric Parameters of Deformed Impinging Droplet in Heat Transfer Calculations

Then the heat transfer from the wall to the droplet is given as:

(12–349)

The effective particle-wall contact area is calculated by time-averaging the particle-wall contact area assuming a sinusoidal particle diameter variation from 0 to the maximum spreading diameter during contact period [65]. The maximum spreading diameter is computed according to [11] as:

(12–350)

(12–351)

The contact time is calculated as [65]:

(12–352)

The heat exchange between the wall and the particle is calculated by integrating Equation 12–349 over the contact time . The increase of the droplet temperature is limited by the boiling point.

For each wall face, the particle-to-wall energy transfer is computed by summing the energy contributions from all particle parcels hitting the wall face and is then added to the heat flux of the wall.