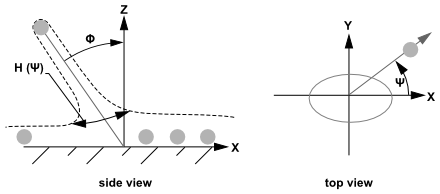
The wall-jet boundary condition provides
a range of rebound directions and velocities when a liquid droplet
collides with a wall. It is suitable for situations where droplets
impact a hot wall, where no liquid film is formed, but the droplets
reflect or stick on the wall depending on their impact properties.
The direction and velocity of the droplet particles are given by the
resulting momentum flux, which is a function of the impingement angle, , and Weber number.
See Figure 12.6: "Wall Jet" Boundary Condition for the Discrete
Phase.
The wall-jet type boundary condition assumes
an analogy with an inviscid jet impacting a solid wall. Equation 12–202 shows the analytical solution for
an axisymmetric impingement assuming an empirical function for the
sheet height () as a function of the angle that the drop leaves
the impingement (
).
(12–202) |
where is the sheet height
at
and
is a constant determined
from conservation of mass and momentum. The probability that a drop
leaves the impingement point at an angle between
and
is given by integrating the expression for
(12–203) |
where is a random number between 0 and 1. The expression
for
is given in Naber and Reitz [468] as
(12–204) |
Fluent uses a simplified expression for computing from Equation 12–204.