The starting point for the development of the Shielded Detached Eddy Simulation (SDES)
shielding function is the existing Delayed Detached Eddy Simulation (DDES) models (see Detached Eddy Simulation (DES)). In DDES, the primary goal is to model the attached and mildly
separated boundary layers in RANS mode and then switch to LES mode for separated (detached) shear
layers. Starting from a given RANS model, a DDES formulation is achieved in two-equation models
by a modification of the sink term in the -equation. In the
-equation of the SST model, the modification is reformulated as follows:
(4–288) |
where
(4–289) |
In the previous equation, is the turbulence length scale,
is the maximum edge length of the local cell,
is the DDES shielding function and
is a coefficient. When
equals zero, the RANS model is recovered. This happens when one or both of the
following conditions are satisfied:
(4–290) |
and/or
(4–291) |
The function is designed to protect attached boundary layers from the switch to the LES
regime. The limit at which the boundary layer becomes affected depends on the ratio of the grid
spacing to the boundary layer thickness (for example,
=
/
). Without shielding (that is, when
=0) the limit is approximately
=1, so that at
<1 the solution in the boundary layer becomes affected by the DES sink term.
With the shielding function as given in Detached Eddy Simulation (DES), the limit for
is reduced to 0.2-0.3, depending on the pressure gradient. Violating these
limits has severe consequences, as the RANS solution will become compromised, and you might not
be aware of it. DES / DDES methods were originally developed for aircraft simulations, where the
boundary layer is typically thin relative to the dimensions of the aircraft / wing. Under those
conditions (and with diligent mesh generation practices), the previously described limits for
can typically be ensured. However, it is harder to ensure these limits for
general industrial applications, due to lower Reynolds numbers, less control over the grid
spacing, and more complex interactions between components.
The first goal of the development of the SDES method was therefore the reformulation of the
function to achieve more reliable shielding, meaning the ability to maintain RANS
boundary layers even under much more severe mesh refinement in attached boundary layers than is
possible for DDES. For this purpose, a new unpublished and Ansys proprietary shielding function
called
was developed, which provides substantially safer shielding than the
functions currently used. The resulting sink term is equivalent to the one from
the DDES model:
(4–292) |
where
(4–293) |
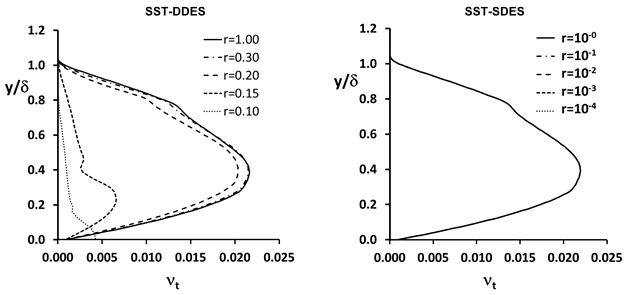
Figure 4.7: Eddy Viscosity Profiles shows the eddy viscosities for self-similar
zero-pressure-gradient boundary layer simulations under mesh refinement, where =
/
(note the different range of the refinement ratio
for the two models). The SDES shielding (on the right) is clearly superior to
the DDES shielding, and maintains the RANS boundary layer even under severe mesh
refinement.