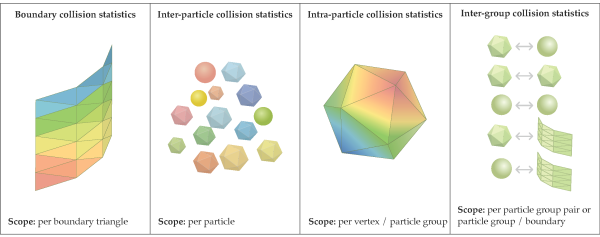
Since Rocky v4.4, four collision statistics modules are available in Rocky. The main difference between them is the spatial scope of the data collection and the way data is associated to geometrical entities for the purpose of visualization and post-processing. This is shown schematically in Figure 4.2: Four built-in collision statistics modules in Rocky..
In the first module, boundary collision statistics, collision data is collected and displayed per boundary triangle. The equivalent module on the particle side is inter-particle collision statistics, in which data is collected and displayed per particle. On the other hand, intra-particle collision statistics only registers collisions involving particles belonging to a given particle group,[3] and associates the data to vertices on its surface, according to the actual position of the collision points relative to the particle. Finally, inter-group collision statistics gathers collision data from all collisions involving a pair of particle groups or a particle group-boundary pair. The specifics of each one of these modules are described later in this chapter.
The lapse of time in which all collision statistics modules collect collision data is the interval between two consecutive output times. Although statistical properties are generated from collision data registered during a data collection interval, they still will be associated to an output time for the purpose of visualization and post-processing. As indicated schematically in Figure 4.3: Data collection time interval., if two output times i and i+1 delimit the data collection interval i, the statistical properties generated from collision data collected in that interval will be associated to the output time i+1. In other words, any statistical property available at a given output time corresponds to the interval delimited by that output time and the previous one.
As mentioned previously, each collision statistics module considers a different geometric entity as a spatial unit for collecting collision data. This spatial unit is called herein data collection region. For instance, on boundary collision statistics, this region is the surface of a triangle making up a boundary. On inter-particle collision statistics, the data collection region is the whole surface of a particle.
It is important to specify what is defined as a collision event in the collision statistics modules available in Rocky. In general, a collision event occurs whenever a particle's surface touches the surface of another particle or a boundary. The collision begins at the instant that an overlap between two surfaces arises, and finishes when that overlap decreases to zero. The values of all variables associated to a collision event are registered only when the collision finishes. Because of that, in long-lasting collisions it is possible that those values may be registered in data collection intervals ahead of the intervals in which the collisions actually began.
Particles with complex shapes, such as concave polyhedral or multi-branched fibers, can touch another particle or boundary at multiple locations. As each of these different contacts can begin at a different time or have a different duration, every one of these contact locations are considered a separate collision event. Multiple contact locations can arise also as a consequence of the discretized representation of the surfaces of particles and boundaries. Such representation includes triangles, edges, and vertices, and whenever any of those entities on one surface touches an entity on another surface, an individual collision event will be registered.
When the boundary collision statistics module is enabled, data from all particle-boundary collisions is collected in order to calculate statistics that will be available for visualization on the surface of boundaries. The data collection units are the boundary triangles in this case. This means that a given statistical value displayed on a boundary triangle is representative of data from all collisions involving that triangle that occurred during a data collection interval.
The available properties in boundary collision statistics are listed in Table 4.1: Available boundary collision statistics, as of v4.4 . When duration, impact velocity or sliding distance are enabled, all four statistics will be available for visualization: mean, standard deviation, skewness, and kurtosis. Herein, the collision duration is defined as the time period in which an actual overlap exists between the two colliding entities. On the other hand, the impact velocity is defined as the relative velocity between the colliding entities at the instant that the contact begins. Moreover, the sliding distance is the distance that a particle moves relative to the boundary during a collision, in a direction parallel to the boundary triangle where the collision occurs.
Table 4.1: Available boundary collision statistics, as of v4.4
|
Property |
Type |
Calculation |
|---|---|---|
|
Duration |
event-based | |
|
Velocity : Impact : Normal |
event-based | Equation 4–1 - Equation 4–4 |
|
Velocity : Impact : Tangential |
event-based | |
|
Sliding Diatance | event-based | Equation 4–1 - Equation 4–4 |
|
Frequency | ||
|
Intensity : Dissipation |
integral-based |
Equation 4–30 using |
|
Intensity : Impact |
integral-based |
Equation 4–30 using |
|
Intensity : Shear |
integral-based |
Equation 4–30 using |
| Intensity | integral-based | Equation 4–30 using |
|
Stress : Normal |
integral-based |
Equation 4–31 using |
|
Stress : Tangential |
integral-based |
Equation 4–31 using |
|
Stress : Adhesive |
integral-based |
Equation 4–31 using |
|
FEM Forces |
integral-based |
In Rocky, intensity is defined as power transferred per unit area. The basis for the calculation of the intensities are the works made by the contact forces during a collision, whose calculation was described in section Works. All forms of intensity provided by boundary collision statistics are computed per boundary triangle, using the following expression:
(4–19) |
where is the area of the boundary triangle and
is the data collection time interval. The sum involves all collisions
occurred during that time interval against the boundary triangle. As specified in , an
intensity will correspond to each work defined in section Works. An
important detail that must be taken into account is that the work used in Equation 4–19 is only the part of the collision work that can be attributed to
the boundary side. The work
in a particle-boundary collision is divided between the particle and the
boundary according to the expressions:
(4–20) |
(4–21) |
where is a splitting factor. For the splitting of both the dissipation and the
impact work, that factor is defined as:
(4–22) |
where and
are the stiffnesses attributed to the particle and the boundary,
respectively, defined similarly to Equation 2–5 and Equation 2–6. Regarding the shear work, it is distributed evenly with a
splitting factor
. Finally, the work
is attributed entirely to the boundary, therefore,
is considered in that case.
Regarding the stresses listed in , the expression used to compute them is equivalent to the one considered for intensities, being necessary only to replace the works by impulses. Therefore, the corresponding expression is:
(4–23) |
where are the impulses, computed using either Equation 4–14
or Equation 4–15.
Boundary collision statistics is able to record also average collision forces acting over boundaries. These forces can be exported to a third-party software to perform structural analysis using the finite element method (FEM). Usually, boundary conditions for that kind of analysis are nodal forces, that is, forces acting on the vertices of the triangles making up the boundaries. Therefore, in order to facilitate the transfer of data to a finite element software, Rocky provides those nodal values of forces, based on collected forces per boundary triangle. These latter ones are determined using the expression:
(4–24) |
where is any of the Cartesian components
of the vector impulse computed with Equation 4–16. As in other
cases, the sum in this equation includes all collisions registered against the boundary
triangle
during the data collection interval
.
In order to obtain the nodal values of force, it is considered that collisions over a boundary triangle are randomly distributed, so the resulting force on the boundary triangle can be split evenly between its three vertices. Therefore, a component of the combined force on one of those vertices will be given by:
(4–25) |
where is the number of triangles surrounding a vertex
, while
is a component of the average force on every one of those triangles,
obtained using Equation 4–24.
FEM forces are the only properties that the boundary collision statistics module associates exclusively to boundary vertices, for both visualization and exportation purposes. All other properties are associated primarily to boundary triangles, although there exists also the option of displaying them as a node-based field representation over the boundary surfaces. For this, vertex values are computed as averages of the values corresponding to the surrounding triangles.
In situations with multiple contact points, the solver applies a factor to reduce the contact forces in order to avoid the collision force growing too much. This reduction factor is applied by the collision statistics during the collision count. That’s why, in some cases, it is possible to have a full collision in one triangle, and a half collision in the next triangle. In order to reduce these situations, you could increase the triangle size.
When the Enable Coarse-Graining checkbox is selected, the following properties calculated by the Boundary Collision Statistics module are modified, in order to account for the CGM scale-up:
Frequency As every contact on the scaled-up system represents
(where
is the CGM scale-factor) contacts in the original system, the computed frequency is multiplied by
.
Duration Time on contacts with CGM scaling-up is increased by a factor of
; therefore, in order to compensate that, the registered duration of each collision is divided by
.
Sliding Distance The sliding distance computed at each collision is divided by
.
The other statistics are kept the same, particularly intensities and stresses, which are integral quantities and are self-similar in this case.
Additionally to the visualization of the spatial distribution of intensities and stresses over the boundary surfaces, Rocky provides also time curves in which each point is the integrated value of a given property over a whole boundary at a given output time. For example, the integration of an intensity over a boundary will give rise to a power curve:
(4–26) |
where is a value of intensity computed with Equation 4–19,
on a triangle of area
located on a boundary
, while
is the number of triangles making up that boundary.
The integration of the stresses over a boundary allows Rocky to determine the total forces acting on it. For instance, the normal force curve is obtained via the integration:
(4–27) |
where is the normal stress computed with Equation 4–23 in the
boundary triangle of area
.
When the Cartesian components of the force are available at the boundary vertices, because they were calculated through Equation 4–25, the components of the total force over a whole boundary are obtained using:
(4–28) |
The intra-particle collision statistics module keeps track of all collisions involving particles that belong to a given particle group. Then, depending on the collision location over a particle's surface, it associates the collected data to a geometric entity of the discretized representation of the surface, for the purposes of visualization. Since all particles in a particle group have the same shape, the statistics can be displayed over the surface of a single particle of the group. However, it is important to note that every value displayed at a given location is representative of all collisions that occurred at that location, on any particle of the group.
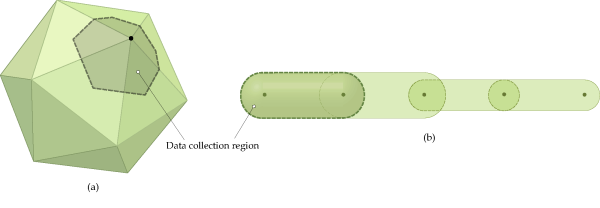
As of v4.4, intra-particle collision statistics is available for polyhedral single-sized rigid particles and for both flexible fibers and flexible solid particles. As illustrated in Figure 4.4: Data collection region for intra-particle collision statistics on (a) rigid polyhedral particles and (b) flexible fibers., the data collection region for polyhedral particles is a non-planar region around a vertex on the particle surface, while for flexible particles it is the whole surface of an element making up the particle. In the case of a polyhedral particle, statistics values are associated to the surface vertices, therefore, the color displayed at a vertex is related to the value attributed to that location. Colors at points other than vertices are determined via interpolation, so the visual representation of the available statistics usually shows a smooth variation over the particle's surface. On the other hand, the statistics calculated for flexible particles are represented as a single color per element.
Figure 4.4: Data collection region for intra-particle collision statistics on (a) rigid polyhedral particles and (b) flexible fibers.
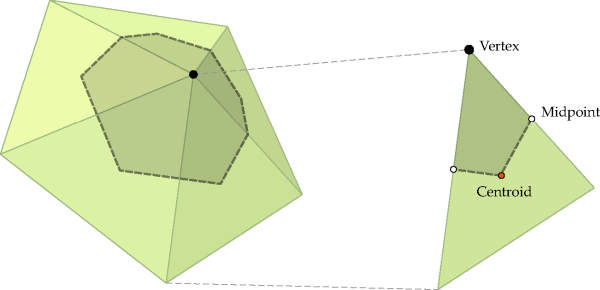
It is worth discussing now the criteria considered to associate the collision data to a vertex in polyhedral particles. The simplest case is when a collision point coincides with a vertex on the particle's surface. Obviously, in that event the data is associated directly to that vertex. On the other hand, if the contact point is located on an edge, the association is made to the nearest vertex on that edge. Moreover, when a collision point is located inside a triangle, a barycentric subdivision of the triangle is considered in order to determine to which vertex the collision data must be associated. In this kind of subdivision, a triangle is divided into three sub-regions of equal area, each one limited by two line segments whose endpoints are the triangle centroid and an edge midpoint, as shown in Figure 4.5: Construction of a data collection region on a polyhedral particle.. If a collision point lies on one of these sub-regions, then the collision data is associated to the corresponding vertex.
lists the available intra-particle collision statistics and the way they are
calculated. The duration and impact velocity statistics are defined and computed exactly in
the same way described in section 1.1,
for the boundary collision statistics module. Regarding the integral-based statistics, there
is an important difference that must be taken into account, however. A value attributed to a
vertex or to an element is the result of the accumulation of collision data coming from,
potentially, all particles belonging to the particle group. Therefore, in order to transform
that cumulative value into an average value representative of a single particle in the
group, we need to divide it by the number of particles that belongs to the group in the
simulation, , at the moment of storing the information. So, for example, the average
collision frequency must be defined as:
(4–29) |
The average impact and dissipation intensities are calculated using the expression:
(4–30) |
where is the area of the data collection region around a vertex, for polyhedral
particles, or the area of the entire surface of an element, for flexible particles.
Equation 4–30 takes into account only the work made by the considered particle. In particle-boundary collisions, the dissipation and the impact work are divided as specified in Equation 4–20 - Equation 4–22. The splitting of those works in particle-particle collisions is made analogously, since it is enough to replace boundary properties by the ones of the second particle in the referred equations. On the other hand, the shear work is distributed evenly between the colliding entities in both particle-boundary and particle-particle collisions.
Finally, the average components of the stress listed in are calculated using the expression:
(4–31) |
where is either the impulse of the normal or the tangential contact force,
calculated as in , or the adhesive impulse, calculated with Equation 4–15 . The other parameters are the same as described above.
Table 4.2: Available intra-particle collision statistics, as of v4.4
|
Property |
Type |
Calculation |
|---|---|---|
|
Duration |
event-based | |
|
Velocity : Impact : Normal |
event-based | |
|
Velocity : Impact : Tangential |
event-based | |
|
Frequency | ||
|
Intensity : Dissipation |
integral-based |
Equation 4–30 using |
|
Intensity : Impact |
integral-based |
Equation 4–30 using |
|
Intensity : Shear |
integral-based |
Equation 4–30 using |
|
Stress : Normal |
integral-based |
Equation 4–31 using |
|
Stress : Tangential |
integral-based |
Equation 4–31 using |
|
Stress : Adhesive |
integral-based |
Equation 4–31 using |
The statistics computed by the inter-particle collision statistics module involves data collected from collisions that occurred on the entire surface of a particle. That is, during a data collection interval, all collisions involving any particle within the simulation will be tracked and the statistics calculated with the collected data will be associated to the particle itself. The generated statistics will appear as additional particle properties in the Rocky UI. They can be visualized on a 3D view window as any other particle property in Rocky, mapping the property value to a color scale.
Table 4.3: Available inter-particle collision statistics, as of v4.4
|
Property |
Type |
Calculation |
|---|---|---|
|
Duration |
event-based | |
|
Velocity : Impact : Normal |
event-based | |
|
Velocity : Impact : Tangential |
event-based | |
|
Frequency | ||
|
Power : Dissipation |
integral-based |
Equation 4–32 using |
|
Power : Impact |
integral-based |
Equation 4–32 using |
|
Power : Shear |
integral-based |
Equation 4–32 using |
|
Force : Normal |
integral-based |
Equation 4–33 using |
|
Force : Tangential |
integral-based |
Equation 4–33 using |
|
Force : Adhesive |
integral-based |
Equation 4–33 using |
lists the current available statistics provided by the inter-particle collision statistics module. All event-based statistics and the collision frequency are calculated as described for boundary collision statistics in section Boundary collision statistics, the only difference is that the data comes from the collisions registered against a particle's surface during a data collection interval.
The dissipation power along with the impact and shear power are calculated using the expression:
(4–32) |
using the appropriate work, as indicated in Table 4.3: Available inter-particle collision statistics, as of v4.4. Again,
the sum will involve all registered collisions against the particle's surface, during the
interval. The same considerations made in section Intra-particle collision statistics regarding the splitting of a collision's
work between particles or particle and boundary apply here.
Similarly, the average normal, tangential, and adhesive forces are computed by means of:
(4–33) |
where is a component of the contact impulse, computed as in Equation 4–14 , or the adhesive impulse, defined in Equation 4–15.
The inter-group collision statistics module classifies all collisions that occurred during a data collection interval, taking into account which group a colliding particle belongs to, Let's remember again that a particle group is a category of particles of the same shape and sharing the same properties. and considering all possible combinations of groups and boundaries.
Let's illustrate this by means of an example: a simulation that includes 3 particle groups (P1, P2, P3), and 2 boundaries (B1, B2). Any collision in that simulation will involve a pair of particles or a pair particle-boundary belonging to one of the 12 combinations listed in Table 4.4: All possible pair combinations for a set of 3 particle groups and 2 boundaries..
Table 4.4: All possible pair combinations for a set of 3 particle groups and 2 boundaries.
| P1 - P1 | P1 - P2 | P1 - P3 | P1 - B1 | P1 - B2 |
| P2 - P2 | P2 - P3 | P2 - B1 | P2 - B2 | |
| P3 - P3 | P3 - B1 | P3 - B2 |
For all or part of such combinations, the inter-group collision statistics module will generate time curves from data collected in all collisions involving particles (or a particle and a boundary) of the given pair. The curves generated by this module are listed together with the built-in particle curves in the Rocky UI.
The available categories of curves in inter-group collision statistics as of v4.4 are listed in Table 4.5: Available curves for intergroup collision statistics, as of v4.4. In the case of the energy curves, each point is obtained by simply summing the corresponding works computed in all collisions registered involving particles (or a boundary) of the corresponding pair, during a data collection interval. Expressed mathematically:
(4–34) |
where is either the dissipation, the impact, or the shear work per collision.
Table 4.5: Available curves for intergroup collision statistics, as of v4.4
|
Property |
Type |
Calculation |
|---|---|---|
|
Duration |
event-based | |
|
Velocity : Impact : Normal |
event-based | |
|
Velocity : Impact : Tangential |
event-based | |
|
Frequency | ||
|
Energy : Dissipation |
integral-based |
Equation 4–34 using |
|
Energy : Impact |
integral-based |
Equation 4–34 using |
|
Energy : Shear |
integral-based |
Equation 4–34 using |
|
Force : Normal |
integral-based |
Equation 4–35 using |
|
Force : Tangential |
integral-based |
Equation 4–35 using |
|
Force : Adhesive |
integral-based |
Equation 4–35 using |
The forces listed in must be interpreted actually as average values of the mean forces acting on all collisions Table 4.5: Available curves for intergroup collision statistics, as of v4.4 involving a given pair, during a data collection interval. The expression used to calculate those average values is:
(4–35) |
where is the corresponding impulse in a collision involving the given pair,
calculated as in either Equation 4–14 or Equation 4–15.
[3] A particle group in Rocky is a category of particles of the same shape and sharing the same properties.