When equations for particles are solved in a reactor model, the total number of variables can be written as

NC = NC_gas + NC_particles

and

NC_particles = {number of Moments or Number of sections} + Number of surface species

Note that when the aggregation model is used, there are additional variables to solve for. For the method of moments, there is one extra variable corresponding to the particle surface area. For the sectional method, the additional number of variables is equal to the number of sections and corresponds to the primary particle number density.

For 0-D closed and open reactor models and for the Plug-Flow reactor, the Particle Tracking feature in Ansys Chemkin solves the coupled system of equations.

For the flame simulators, the total number of variables becomes NC*NP where NP is the number of grid points. Since a typical gas-phase reaction mechanism contains hundreds of species, the number of variables in the gas phase is typically much larger than the number of variables for the particles. Effectively, the solution of the gas-phase equations consumes the larger portion of the overall computational time. This technique iteratively solves the two (gas and particle) problems separately. Doing so allows the use of advanced solution techniques for the gas-phase problem. As long as the coupling between the gas phase and the particles is relatively weak, the iterations converge rapidly, such that the overall convergence time is reduced. A relaxation factor can be used in cases where the coupling is strong.

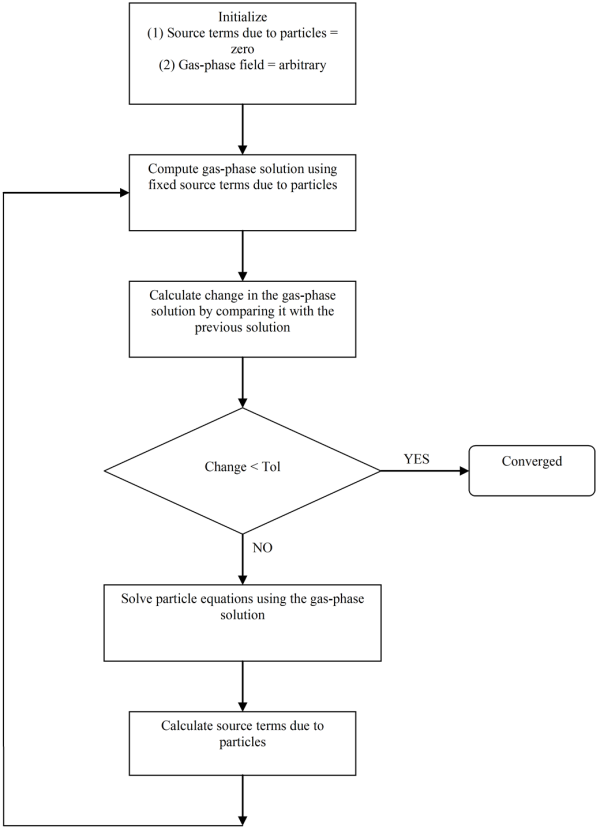
The iteration algorithm is as follows:

Convergence is determined when the change in the computed gas-phase solution is below a user-specified tolerance.

Figure 19.17: Flowchart of segregated solver

Figure 19.18: Steps in solution for particle equations for sectional model in flame simulations

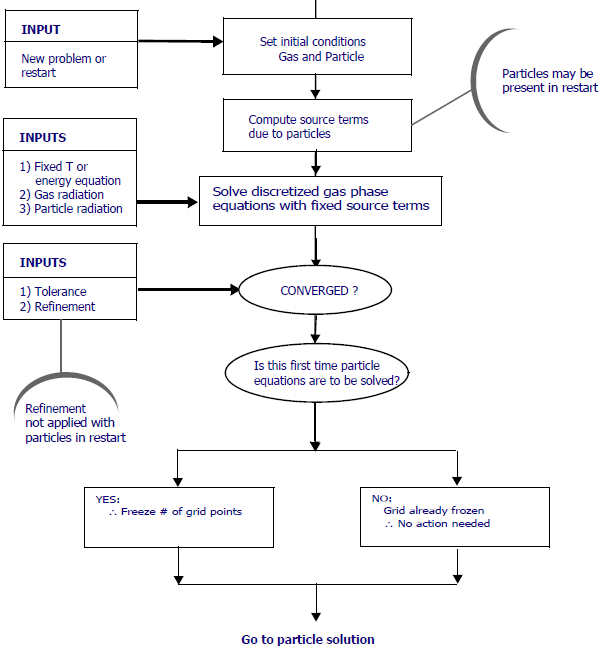
Figure 19.19: Expanding steps in solution for particle equations for sectional model in flame simulations