Soot particle samples collected from the exhaust of practical combustion devices are found to be mostly fractal aggregates rather than spherical primary particles. This is also true for other industrial processes such as production of titania (TiO₂) in a tubular reactor. The omnipresence of particles as aggregates, regardless of where and from which processes they are formed, creates the necessity of an aggregation model for use with the Particle Tracking feature.

The particle-particle aggregation process can be modeled as a sequence of collision, sticking, and complete coalescence by fusion, which is also called sintering. After a collision of two particles that results in particles sticking to each other, we assume that the contact between the particles is initially a point contact. The individual particles are then called primary particles of a single aggregate. (In the literature, an aggregate is sometimes also referred to as an agglomerate.) The total mass and the total surface area are both conserved at this stage. For a constant material density for the particles, the total volume is also conserved. As a result of processes such as grain-boundary diffusion, the particles that are stuck together proceed to sinter or fuse together and eventually completely coalesce to form a single particle. Thus, at the end of the coalescence process, the total mass (volume) is conserved but surface area is not. Figure 19.14: Schematic showing correlations of the final collision states and measurable aggregate properties illustrates this process.

Figure 19.14: Schematic showing correlations of the final collision states and measurable aggregate properties

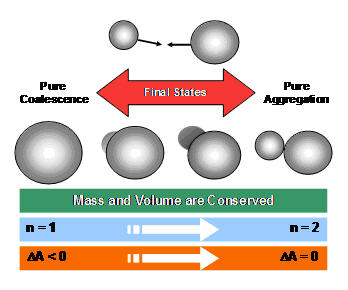
It can be noted that the colliding aggregates may not completely coalesce for a given time scale, that is, two particles colliding may not become a single sphere. In general, not all primary particles from a given aggregate are of the same size and not all primary particles are truly spherical. However, this approximation is necessary for a computationally feasible representation. Aggregates may also contain different numbers of primary particles. Figure 19.15: Aggregation and coalescence of two particles (general case) illustrates the case where two colliding aggregates have four and two primary particles, respectively, leading to a new aggregate formed after the collision that initially has six primary particles. After complete coalescence, however, a single spherical (primary) particle is formed from the aggregate similar to the final particle in Figure 19.14: Schematic showing correlations of the final collision states and measurable aggregate properties . Table 19.1: Size distribution property changes due to aggregation. NP, A, and V indicate the number of primary particles, the surface area, and the volume (directly related to mass), respectively summarizes changes in various quantities caused by the process illustrated in Figure 19.15: Aggregation and coalescence of two particles (general case) .

Figure 19.15: Aggregation and coalescence of two particles (general case)