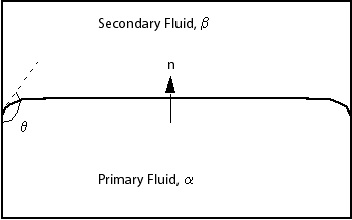
The surface tension model used in CFX is based on the Continuum Surface Force model of Brackbill et al. [27]. This models the surface tension force as a volume force concentrated at the interface, rather than a surface force. Consider the free surface interface shown in the figure below:

Figure 5.1: Free Surface Interface

Define a Primary Fluid (the liquid phase) and a Secondary Fluid (usually a gas phase). The surface tension force given by the Continuum Surface Force model is:

(5–290)

where:

(5–291)

(5–292)

where is the surface tension coefficient, is the interface normal vector pointing from the primary fluid to the secondary fluid (calculated from the gradient of a smoothed volume fraction), is the gradient operator on the interface and is the surface curvature defined by:

(5–293)

The two terms summed on the right hand side of Equation 5–291 reflect the normal and tangential components of the surface tension force respectively. The normal component arises from the interface curvature and the tangential component from variations in the surface tension coefficient (the Marangoni effect).

The term is often called the interface delta function; it is zero away from the interface, thereby ensuring that the surface tension force is active only near to the interface.

When the interface between the two fluids intersects a wall, it is possible to account for wall adhesion by specifying the contact angle, , which the interface makes with the wall through the primary fluid. The interface normal vector used for the calculations of both curvature and the surface tension force must satisfy the wall contact angle.