16.2.12. Variables and Predefined Expressions Available in CEL Expressions

The following is a table of the more common variables and predefined expressions that are available for use with CEL when defining expressions. To view a complete list, open the Expressions workspace. For an explanation of the column headings, see List of Field Variables.

Many variables and expressions have a long and a short form (for example, Pressure or p).

Additional Variables and expressions are available in CFD-Post. For details, see CFX Expression Language (CEL) in CFD-Post in the CFD-Post User's Guide.

Table 16.1: Common CEL Single-Value Variables and Predefined Expressions

Long Variable Name	Short Variable Name	Units	Availability	Definition
Accumulated Coupling Step	acplgstep	[ ]	2 C	These single-value variables enable access to timestep, timestep interval, and iteration number in CEL expressions. They may be useful in setting parameters such as the Physical Timescale via CEL expressions. For details, see Timestep, Timestep Interval, and Iteration Number Variables.
Accumulated Iteration Number	aitern	[ ]	2 C
Accumulated Time Step	atstep	[ ]	2 C
Current Iteration Number	citern	[ ]	2 C
Current Stagger Iteration	cstagger	[ ]	2 C
Current Time Step	ctstep	[ ]	2 C
Sequence Step	sstep	[ ]	2 C
Time Step Size	dtstep	[s]	2 C
Time	t	[s]	2 C

Note: Variables with names shown in bold text in the tables that follow are not output to CFD-Post. However, some of these variables can be output to CFD-Post by selecting them from Extra Output Variables List on the Results tab of the Solver > Output Control details view in CFX-Pre.

Table 16.2: Common CEL Field Variables and Predefined Expressions

Long Variable Name	Short Variable Name	Units	Availability	Definition
Axial Distance	aaxis	[m]	2 C	Axial spatial location measured along the locally-defined axis from the origin of the latter. When the locally-defined axis happens to be the Z axis, z and aaxis are identical.
Absorption Coefficient	absorp	[m^-1]	1 C, M, R, TS	The property of a medium that describes the amount of absorption of thermal radiation per unit path length within the medium. It can be interpreted as the inverse of the mean free path that a photon will travel before being absorbed (if the absorption coefficient does not vary along the path).
Boundary Distance	bnd distance	[m]	2 A, C, M, R, TS
Boundary Scale	bnd scale	[m^-2]	3 C, M, R, TS
Contact Area Fraction	af	[ ]	3 M
[AV name]	[AV name]			Additional Variable name
Thermal Expansivity	beta	[K^-1]	2 C
Effective Density	deneff	[kg m^-3]	3 A, C, M, R, TS
Density	density	[kg m^-3]	2 A, C, M, P, R, TS
Turbulence Eddy Dissipation	ed	[m^2 s^-3]	1 A, C, M, P, R, TS
Eddy Viscosity	eddy viscosity	[kg m^-1 s^-1]	1 A, C, M, P, R, TS
Emissivity	emis	[ ]	1 C	A characteristic of a surface that describes the fraction of emitted radiation with respect to the blackbody emission at the same temperature.
Extinction Coefficient	extinct	[m^-1]	1 C	The property of a medium that describes the amount of absorption and scattering of thermal radiation per unit path length for propagation in the medium.
Initial Cartesian Coordinates	initcartcrd	[m]	2 C	The position of each node as it was at the start of the simulation (that is, the current position with Total Mesh Displacement subtracted). The individual components are referred to as "Initial X", "Initial Y" and "Initial Z".
Turbulence Kinetic Energy	ke	[m^2 s^-2]	1 A, C, M, P, R, TS
Mach Number	Mach	[ ]	1 A, C, M, R, TS
Mach Number in Stn Frame	Machstn	[ ]	1 A, C, M, R, TS	Mach Number in Stationary Frame
Mass Concentration	mconc	[m^-3 kg]	2 A, C, M, P, R, TS	Mass concentration of a component
Mass Fraction	mf	[ ]	1 A, C, M, P, R, TS
Conservative Mass Fraction	mfc	[ ]	2 A, C, M, R, TS
Mean Particle Diameter	mean particle diameter	[m]	3 C, P
Mesh Displacement	meshdisp	[m]	3 C, M, R, TS	The displacement relative to the previous mesh
Mesh Expansion Factor	mesh exp fact	[ ]	2 C, M, R, TS	Ratio of largest to smallest sector volumes for each control volume.
Mesh Initialisation Time	meshinittime	[s]	2 C	Simulation time at which the mesh was last re-initialized (most often due to interpolation that occurs as part of remeshing)
Mixture Fraction	mixfrc	[ ]	1 A, C, M, R, TS	Mixture Fraction Mean
Mixture Model Length Scale	mixture length scale	[m]	3 M
Mixture Fraction Variance	mixvar	[ ]	1 A, C, M, R, TS
Molar Concentration	molconc	[m^-3 mol]	2 A, C, M, P, R, TS
Molar Fraction	molf	[ ]	2 A, C, M, P, R, TS
Molar Mass	mw	[kg mol^-1]	3 C, P
Orthogonality Angle	orthangle	[rad]	2 C, M, R, TS	A measure of the average mesh orthogonality angle
Orthogonality Angle Minimum	orthanglemin	[rad]	2 C, M, R, TS	A measure of the worst mesh orthogonality angle
Orthogonality Factor	orthfact		2 C, M, R, TS	A non-dimensional measure of the average mesh orthogonality
Orthogonality Factor Minimum	orthfactmin		2 C, M, R, TS	A measure of the worst mesh orthogonality angle
Pressure	p	[kg m^-1 s^-2]	1 A, C, M, P, R, TS
Absolute Pressure	pabs	[kg m^-1 s^-2]	2 A, C, M, R, TS
Reference Pressure	pref	[kg m^-1 s^-2]	2 C	The `Reference Pressure` is the absolute pressure datum from which all other pressure values are taken. All relative pressure specifications in CFX are relative to the `Reference Pressure`. For details, see Setting a Reference Pressure in the CFX-Solver Modeling Guide.
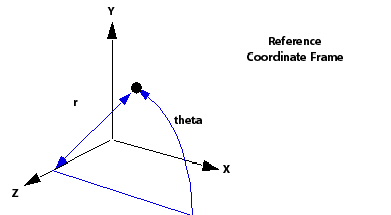
Distance from local Z axis	r	[m]	2 C	Radial spatial location. . For details, see CEL Variables r and theta.
Radius	raxis	[m]	2 C	Radial spatial location measured normal to the locally-defined axis. When the locally-defined axis happens to be the Z axis, r and raxis are identical.
Radiative Emission	rademis	[kg s^-3]	1 RA	Blackbody radiative emission is defined as * Refractive Index^2 * Temperature^4, where represents the Stefan-Boltzmann constant.
Incident Radiation	radinc	[kg s^-3]	1 C, DT, M, R, TS	This is a volumetric quantity and has no relevance at boundaries. For relevant radiation quantities at boundaries, see the definitions for `Wall Radiative Heat Flux` and `Wall Irradiation Flux` in Variables Relevant for Radiation Calculations.
Radiation Intensity	radint	[kg s^-3]	1 A, C, M, P, R, TS	This is written to the results file for all radiation models. For Monte Carlo simulations, the `Radiation Intensity.Normalized Std Deviation` is also written. This variable represents the statistical deviation with respect to the mean for the Monte Carlo model.
Refractive Index	refrac	[ ]	1 C, R, TS	A non-dimensional parameter defined as the ratio of the speed of light in a vacuum to that in a material.
Non dimensional radius	rNoDim	[ ]	2 C	Non-dimensional radius (available only when a rotating domain exists). For details, see CEL Variable rNoDim.
Reynolds Stress	rs uu, rs vv, rs ww, rs uv, rs uw, rs vw	[m^2 s^-2]	2 A, C, M, P, R, TS	The six Reynolds Stress components
Statistical Reynolds Stress	rsstat uu, rsstat vv, rsstat ww, rsstat uv, rsstat uw, rsstat vw	[m^2 s^-2]	3 M, R	The six Statistical Reynolds Stress components
Scattering Coefficient	scatter	[m^-1]	1 C, M, R, TS	The property of a medium that describes the amount of scattering of thermal radiation per unit path length for propagation in the medium. It can be interpreted as the inverse of the mean free path that a photon will travel before undergoing scattering (if the scattering coefficient does not vary along the path).
Soot Mass Fraction	sootmf	[ ]	1 A, C, M, R, TS
Soot Nuclei Specific Concentration	sootncl	[m^-3]	1 A, C, M, R, TS
Specific Volume	specvol	[m^3 kg^-1]	3 A, C, M, R, TS
Local Speed of Sound	speedofsound	[m s^-1]	2 C, M, R, TS
Subdomain	subdomain	[ ]	2 C	Subdomain variable (1.0 in subdomain, 0.0 elsewhere). For details, see CEL Variable "subdomain" and CEL Function "inside".
inside() @<Locations>	inside() @<Locations>			inside variable (1.0 in subdomain, 0.0 elsewhere). For details, see CEL Variable "subdomain" and CEL Function "inside".
Theta	taxis	[rad]	2 C	taxis is the angular spatial location measured around the locally-defined axis, when the latter is defined by the Coordinate Axis option. When the locally defined axis is the z(/x/y)-axis, taxis is measured from the x(/y/z)-axis, positive direction as per right-hand rule.
Turbulence Eddy Frequency	tef	[s^-1]	1 A, C, M, P, R, TS
Angle around local Z axis	theta	[rad]	2 C	Angle, arctan(y/x). For details, see CEL Variables r and theta.
Total Mesh Displacement	meshdisptot	[m]	1 C, DT, M, R, TS	The total displacement relative to the initial mesh
Velocity u Velocity v Velocity w	u v w	[m s^-1]	1 A, C, M, P, R, TS	Velocity in the x, y, and z coordinate directions
Velocity in Stn Frame u Velocity in Stn Frame v Velocity in Stn Frame w	velstn u velstn v velstn w	[m s^-1]	1 A, C, M, R, TS	Velocity in Stationary Frame in the x, y, and z coordinate directions
Volume Fraction	vf	[ ]	1 A, C, M, P, R, TS
Conservative Volume Fraction	vfc	[ ]	2 A, C, M, R, TS	The variable `<fluid>.Conservative Volume Fraction` should not usually be used for postprocessing.
Kinematic Viscosity	visckin	[m^2 s^-1]	2 A, C, M, P, R, TS
Wall Distance	wall distance	[m]	2 A, C, M, P, R, TS
Wall Power Density	wall powerdens	[W m^-2]	2 C, DT, R, TS	Time rate of work done by a wall moving against the contacting fluid, per unit of wall area This quantity is intended primarily for use in blade flutter analysis. The wall motion considered is measured in the same frame of reference as the blade (whether rotating or stationary). Only the component of wall motion normal to the wall surface is considered. The component of wall motion tangential to the wall surface is neglected. This variable is 0 at stationary walls.
Wall Work Density	wall workdens	[J m^-2]	2 C, DT, R, TS	Work done by a wall moving against the contacting fluid, per unit wall area, over the current time step This quantity is intended primarily for use in blade flutter analysis. The wall motion considered is measured in the same frame of reference as the blade (whether rotating or stationary). Only the component of wall motion normal to the wall surface is considered. The component of wall motion tangential to the wall surface is neglected. This variable is 0 at stationary walls.
Wall Periodic Work Density	wall perworkdens	[J m^-2]	2 C, DT, R, TS	Work done by a wall moving against the contacting fluid, per unit wall area, over one vibration period This quantity is intended primarily for use in blade flutter analysis. The wall motion considered is measured in the same frame of reference as the blade (whether rotating or stationary). Only the component of wall motion normal to the wall surface is considered. The component of wall motion tangential to the wall surface is neglected. This quantity is computed based on Fourier coefficient data. This variable is 0 at stationary walls.
Wall Scale	wall scale	[m^2]	3 M, R, TS

16.2.12.1. System Variable Prefixes

In order to distinguish system variables of the different components and fluids in your CFX model, prefixes are used. For example, if carbon dioxide is a material used in the fluid air, then some of the system variables that you might expect to see are:

air.density - the density of air
air.viscosity - the viscosity of air
air.carbondioxide.mf - the mass fraction of carbon dioxide in air
air | water.surface tension coefficient – the surface tension coefficient between air and water
air | water.area density – the interfacial area density between air and water.

In a single phase simulation the fluid prefix may be omitted.

For multiphase cases, a fluid prefix indicates either a specific fluid, or a specific fluid pair. The absence of a prefix indicates a bulk or fluid independent variable, such as pressure.

For porous solids, those variables that exist in the solid are prefixed by the name of the solid phase.

16.2.12.2. CEL Variables r and theta

r is defined as the normal distance from the third axis with respect to the reference coordinate frame. theta is defined as the angular rotation about the third axis with respect to the reference coordinate frame. For details, see Coordinate Frames in the CFX-Solver Modeling Guide.

The variables Radius and theta are available only when the rotational axis has been defined. The rotational axis can either be defined in the results file or in CFD-Post through the Initialization panel in the Turbo workspace.

Note: theta is expressed in radians and will have values between and .

r and theta are particularly useful for describing radial distributions, for instance the velocity profile at the inlet to a pipe.

Figure 16.1: r and theta with Respect to the Reference Coordinate Frame

16.2.12.3. CEL Variable rNoDim

rNoDim is a dimensionless system variable that can be useful for rotating machinery applications. It is a ratio of radii, defined to be zero at the minimum radius and unity at the maximum radius, so that in general:

where R is the radius of any point in the domain from the axis of rotation. rNoDim is only available for domains defined with a rotating frame of reference.

16.2.12.4. CEL Variable "subdomain" and CEL Function "inside"

subdomain is essentially a step function variable, defined to be unity within a subdomain and zero elsewhere. This is useful for describing different initial values or fluid properties in different regions of the domain. It works in all subdomains but cannot be applied to specific subdomains (for example, an expression for temperature in a subdomain could be 373*subdomain [K]).

The inside CEL function can be used in a similar way to the subdomain variable, but allows a specific 2D or 3D location to be given. For example, 273 [K] * inside()@Subdomain 1 has a value of 273 [K] at points in Subdomain 1 and 0 [K] elsewhere. Furthermore, the location can be any 2D or 3D named sub-region of the physical location on which the expression is evaluated. The location can also be an immersed solid domain.

16.2.12.5. Timestep, Timestep Interval, and Iteration Number Variables

These variables enable access to timestep, timestep interval, and iteration number in CEL expressions. They may be useful in setting parameters such as the Physical Timescale via CEL expressions.

16.2.12.5.1. Steady-State Runs

In steady-state runs, only Accumulated Iteration Number (or, equivalently Accumulated Time Step) and Current Iteration Number (or, equivalently Current Time Step) are of use. Current Iteration Number gives the outer iteration number of the current run. The outer iteration number begins at 1 for each run, irrespective of whether it is a restarted run. Accumulated Iteration Number gives the accumulated outer iteration number, which accumulates across a restarted run.

16.2.12.5.2. Transient Runs

In transient runs, Accumulated Time Step and Current Time Step are used for the accumulated and current timestep numbers of the outer timestep loop. Current Iteration Number gives the current coefficient loop number within the current timestep. Thus, Current Iteration Number will cycle between 1 and n for each timestep during a transient run, where n is the number of coefficient loops. Accumulated Iteration Number is equivalent to Current Iteration Number for transient runs.

16.2.12.5.3. Timestep Variables in CFD-Post

In CFD-Post, Sequence Step (sstep) is the 'global' sequence timestep. It is equivalent to the Step value in Timestep Selector in the CFD-Post User's Guide.

Accumulated Time Step (atstep) and Current Time Step (ctstep) are available for both steady-state and transient runs, with Current Time Step being set to the same value as Accumulated Time Step.

Accumulated Iteration Number (aitern), Current Iteration Number (citern), Accumulated Coupling Step (acplgstep), and Current Stagger Iteration (cstagger) are not available in CFD-Post.

If multiple cases are loaded, the values obtained from evaluating these timestep-related variables relate to the last loaded case.

16.2.12.6. Expression Names

Your CEL expression name can be any name that does not conflict with the name of a CFX system variable, mathematical function, or an existing CEL expression. The RULES and VARIABLES files provide information on valid options, variables, and dependencies. Both files are located in <CFXROOT>/etc/ and can be viewed in any text editor.

16.2.12.7. Scalar Expressions

A scalar expression is a real valued expression using predefined variables, user variables, and literal constants (for example, 1.0). Note that literal constants have to be of the same dimension. Scalar expressions can include the operators + - * / and ^ and several of the mathematical functions found in standard Fortran (for example, sin() and exp()).

An expression’s value is a real value and has specified dimensions (except where it is dimensionless - but this is also a valid dimension setting).

For example, if t is time and L is a length then the result of L/t has the same dimensions as speed.

The + and - operators are only valid between expressions with the same dimensions and result in an expression of those dimensions.

The * and / operators combine the dimensions of their operands in the usual fashion. X^I, where I is an integer, results in an expression whose dimensions are those of X to the power I. The trigonometric functions all work in terms of an angle in radians and a dimensionless ratio.

16.2.12.8. Expression Properties

There are three properties of expressions:

An expression is a simple expression if the only operations are +, -, *, / and there are no functions used in the expression.
An expression is a constant expression if all the numbers in the expression are explicit (that is, they do not depend on values from the solver).
An expression is an integer expression if all the numbers in the expression are integers and the result of each function or operation is an integer.

For example, (3+5)/2 is a simple, constant, integer expression. However, 2*(1/2) is not a constant integer expression because the result of 1/2 is 0.5, not an integer. Also 3.*4 is not a constant integer expression because 3 is not an integer. Moreover, 2^3 is not a simple, constant, integer expression because ^ is not in the list (+, -, *, /).

Expressions are evaluated at run time and in single precision floating point arithmetic.

16.2.12.9. Available and Unavailable Variables

CFX System Variables and user-defined expressions will be available or unavailable depending on the simulation you are performing and the expressions you want to create. In some circumstances, System Variables are logically unavailable; for instance, time (t) is not available for steady-state simulations. In others, the availability of a System Variable is not allowed for physical model reasons. For example, density can be a function of pressure (p), temperature (T) and location (x, y, z), but no other system variables.

Information on how to find dependencies for all parameters is available in the RULES and VARIABLES files. Both files are located in <CFXROOT>/etc/ and can be viewed in any text editor.

The expression definition can depend on any system variable. If, however, that expression depends on a system variable that is unavailable for a particular context, then that expression will also be unavailable.