The Gray model assumes that all radiation quantities are uniform throughout the spectrum. This simplifies the radiation calculation considerably because fewer equations should be solved. For combustion calculations, where certain gases are absorbing in finite regions of the spectrum and transparent for rest, it will introduce errors in the total radiative heat flux.

The Multiband model discretizes the spectrum into bands of finite width and assumes that radiation quantities are nearly uniform within the band. The total radiative heat flux is computed by adding the results within each band. Each spectral band can be defined by different means: Frequency, Wavelength in Vacuum, or Wavenumber in Vacuum.

At least two different spectral bands must be set. The solver will check that the union of all spectral bands fully covers the thermal radiation part of spectrum and that they do not overlap. The wavenumber range should cover at least the range between 100 [cm^-1] and 100,000 [cm^-1] to cover the full thermal spectrum. A warning message will be written to the CFX-Solver Output file otherwise.

When using CEL expressions to describe the spectral variation of any radiation quantity, the solver will use the frequency for the spectral band.

This model assumes that gas absorption can be represented by a weighted sum of gray media. The weights and absorption coefficients have been correlated in the literature for a variety of gases (see Modest [8]). The current implementation does not provide a specific set of weights or coefficients, though there is a CFX-Pre template available. Therefore, you must specify the weights/amplitudes and the absorption coefficients for each gray gas.

Caution should be taken when specifying the set of coefficients:

A Multigray CCL Template is available in the Library mode of CFX-Pre. For details, see Multigray Radiation in the CFX-Pre User's Guide.

Although it is convenient to average radiation properties over the whole spectrum (Gray model), real gases only absorb and emit in discrete bands. Upon diffuse reflection at walls, radiation emitted by the gases within discrete bands is re-emitted at all wavelengths as thermal radiation with the characteristic blackbody spectrum. Although much of this reflected radiation will be reabsorbed by the gases, some will now lie outside the absorption bands of any of the gases present and will therefore pass through the gas volume without absorption.

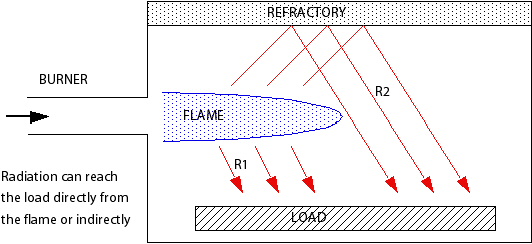
This effect can be significant when it is important to distinguish between emission from gases and wall reflection, for example, in a reheat furnace, see Figure 10.1: Example of a Reheat Furnace, where a thermal load is being heated directly by a gaseous flame (R1) and indirectly by a refractory wall (R2). If the emissivity of the refractory wall is increased (for example, by a special coating), the proportion of radiation with wavelengths outside the gaseous absorption bands increases and the intensity of radiation reaching the load becomes higher. If the radiative heat transfer in the reheat furnace is modeled using a Gray spectral model, then this effect would not be correctly predicted. The Multiband, and Multigray/Weighted Sum of Gray Gases models include a clear band and correctly predict an increase of radiative heat transfer to the load, as wall emissivity increases in the reheat furnace example.

Figure 10.1: Example of a Reheat Furnace

A more obvious limitation of the Gray model in combustion calculations is that a single absorption coefficient is set, independent of the local gas composition. This implies that the combustion air has the same radiative properties as the combustion products, although the latter contains a high percentage of and , which are highly efficient emitters of thermal radiation. The actual error caused by this approximation is not usually large because combustion air is usually at much lower temperatures than the products but, nevertheless, it leads to an overestimate of the absorption due to the air.